Хелпикс

Главная

Контакты

Случайная статья



Вычисление площадей с помощью определенного интеграла.

Стр 1 из 3Следующая ⇒


Вычисление площадей с помощью определенного интеграла.

Разберем типовую и наиболее распространенную задачу – как с помощью определенного интеграла вычислить площадь плоской фигуры. Наконец-то ищущие смысл в высшей математике – да найдут его. Придется вот в жизни приближать дачный участок элементарными функциями и находить его площадь с помощью определенного интеграла.

Для успешного освоения материала, необходимо:

1) Разбираться в неопределенном интеграле хотя бы на среднем уровне.

2) Уметь применять формулу Ньютона-Лейбница и вычислять определенный интеграл.

В действительности, для того чтобы находить площадь фигуры не надо так уж много знаний по неопределенному и определенному интегралу. Задание «вычислить площадь с помощью определенного интеграла» всегда предполагает построение чертежа, поэтому гораздо более актуальным вопросом будут ваши знания и навыки построения чертежей. В этой связи полезно освежить в памяти графики основных элементарных функций, а, как минимум, уметь строить прямую, параболу и гиперболу.

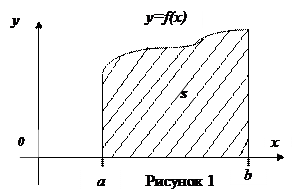
1. Если на отрезке [a; b] функция 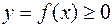, то площадь криволинейной трапеции, ограниченной сверху кривой , снизу осью 0X, справа и слева прямым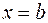и и 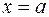(рисунок 1), вычисляется по формуле:

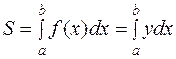(4.1)

 

 

 

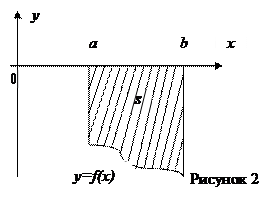
2. Если 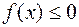на отрезке [a; b], то площадь фигуры (рисунок 2) вычисляется по формуле:

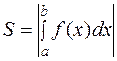(4.2)

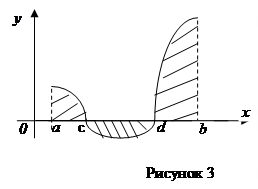
3. Если функция 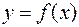меняет знак на отрезке [a; b], то площадь фигуры (рисунок 3) вычисляется по формуле:

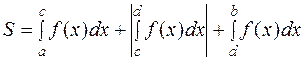, (4.3)

где интегралы по отрезкам, на которых функция отрицательна, берутся по абсолютной величине.

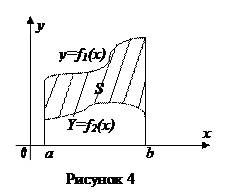
4. Если на одном и том же отрезке [a; b] заданы две функци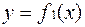и: и 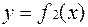, причем 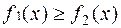для любых 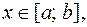то площадь фигуры (рисунок 4) вычисляется по формуле:

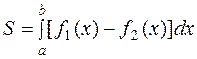(4.4)


123Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.