Хелпикс

Главная

Контакты

Случайная статья



Задача 1. Найти область определения функции .

⇐ ПредыдущаяСтр 3 из 4Следующая ⇒


Решение типового варианта.

Задача 1. Найти область определения функции    .

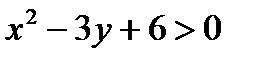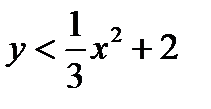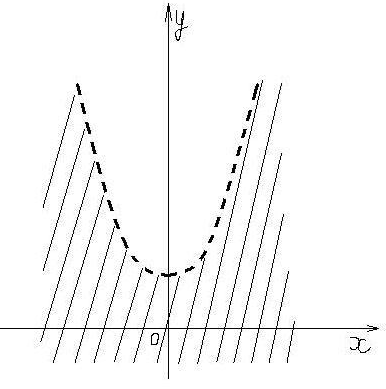
Решение.Логарифмическая функция определена только при положительном значении аргумента, поэтому  или   . Границей области определения будет линия 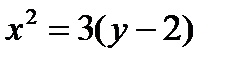  (парабола). Парабола разбивает плоскость на внутреннюю и внешнюю часть. Областью определения функции будут являться точки плоскости, лежащие вне параболы. Точки, лежащие на параболе в область определения функции не входят, так как неравенство  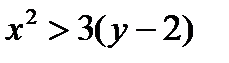  не строгое. На рисунке точки, являющиеся областью определения функции отмечены штриховкой.

        

 

      Задача 2. Указать с помощью градиента направление наибольшей скорости возрастания функции 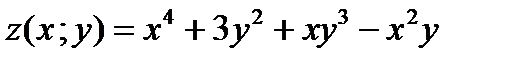  в данной точке .

 

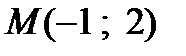Решение. Направление наискорейшего возрастания функции в заданной точке находится с помощью градиента:

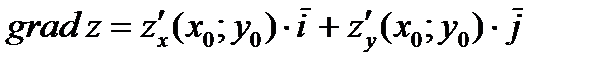
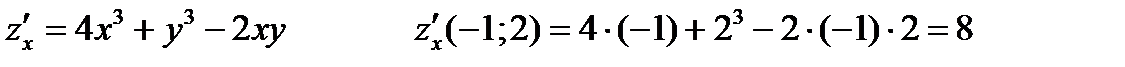
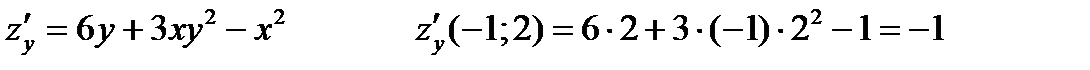
Таким образом, направление наибольшей скорости возрастания функции 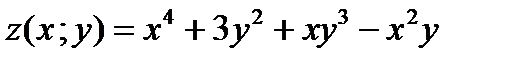  в точке  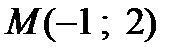указывает вектор .

 

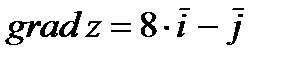Задача 3.  Вычислить значения частных производных функции 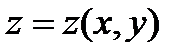, заданной неявно уравнением  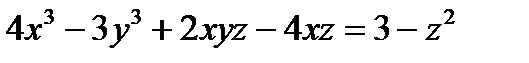в точке 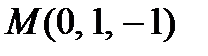с точностью до двух знаков после запятой.

Решение.  В данном случае 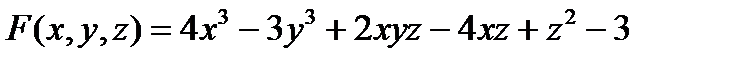, поэтому:

,       ,         .

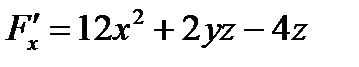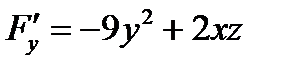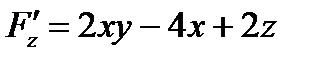Следовательно:

,       .

 

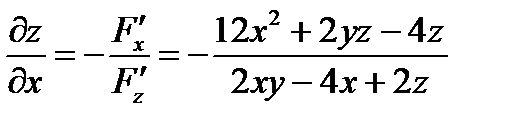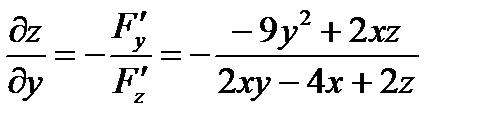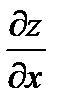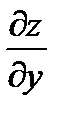Вычисляем значение  и  в точке 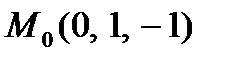, подставляем в частные производные :

 ,   .

 

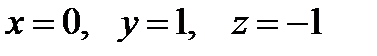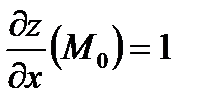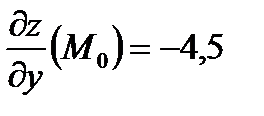           Задача 4.  Исследовать на экстремум функцию .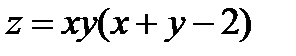

    Решение.  Находим первые частные производные функции:

 ,     .

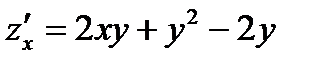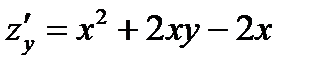Приравнивая их к нулю, получаем систему уравнений:

 ,   ,

   

                                   

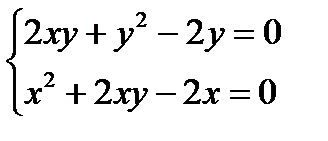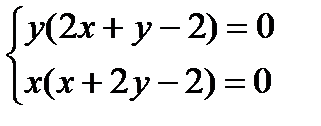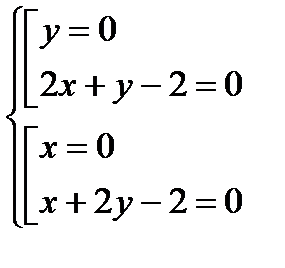
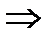
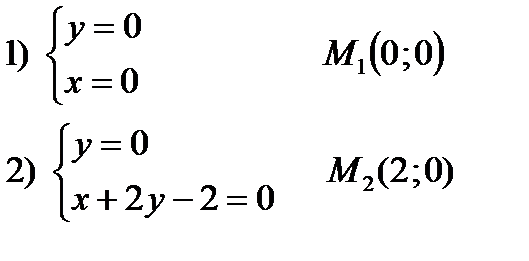
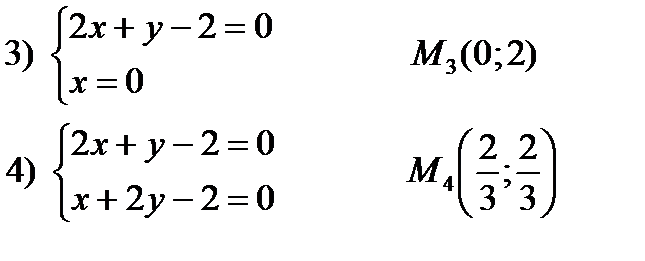
Стационарные точки данной функции:

, , , .

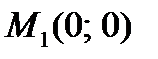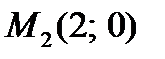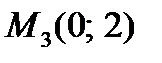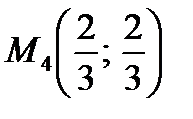Для определения достаточных условий максимума и минимума найдем вторые частные производные:

,     ,     .

,       ,       .

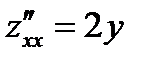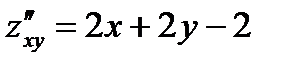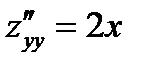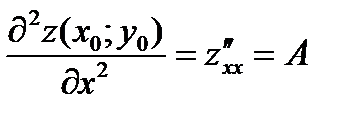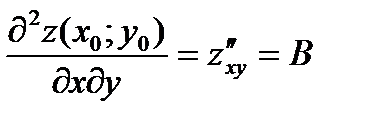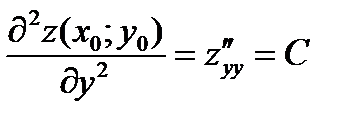Составим .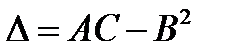

.

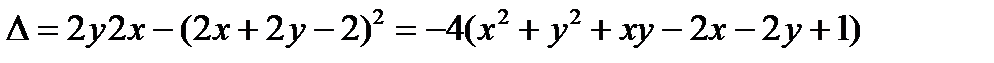1) Для точки 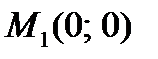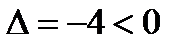, т.е. экстремума нет;

2) Для точки 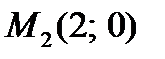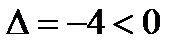, т.е. экстремума нет;

3) Для точки 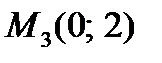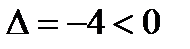, т.е. экстремума нет;

4) Для точки 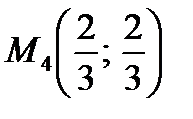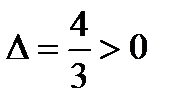, при этом 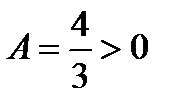, т.е. имеем точку минимума, в которой .

 

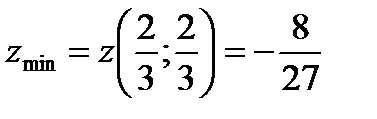Задача 5.  Найти вторые частные производные функции 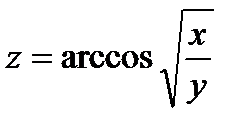. Убедиться в том, что .

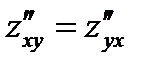Решение. Вначале находим первые частные производные данной функции:

;

.

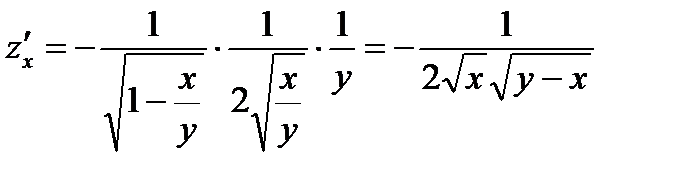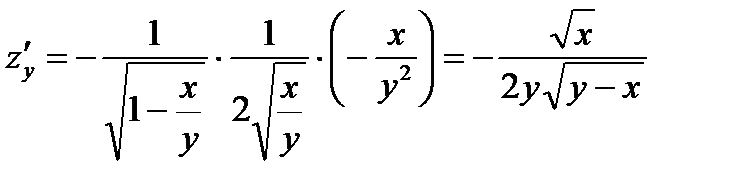    Дифференцируя каждую из полученных производных 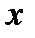по  и по 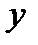 находим вторые частные производные данной функции:

;

;

;

.

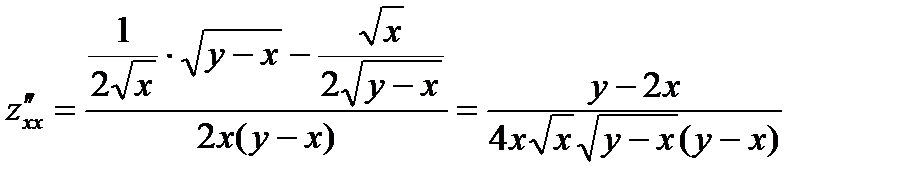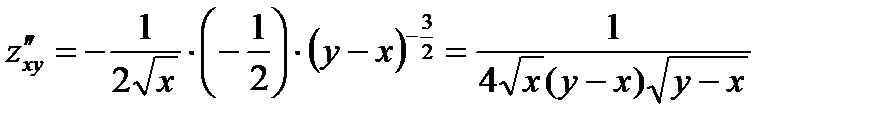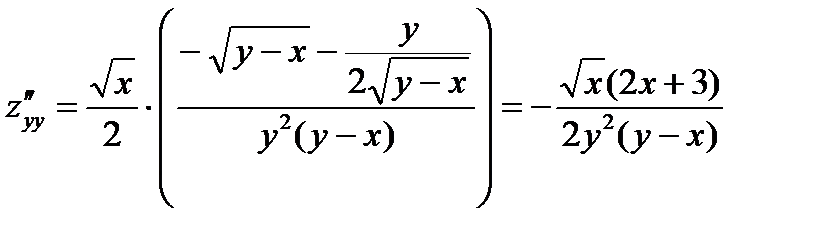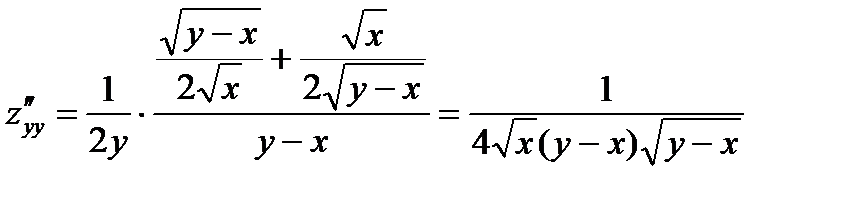Как видно, смешанные частные производные 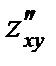  и 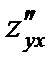  равны.

Задача 6.  Найти уравнения касательной плоскости и нормали к заданной поверхности 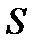: 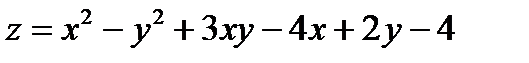в  точке .

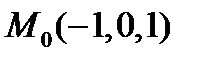Решение.  Находим частные производные:

,   .

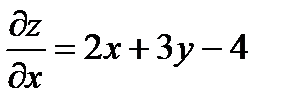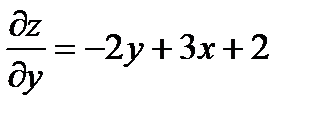    Подставляя в полученные выражения координаты точки 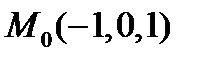 находим:

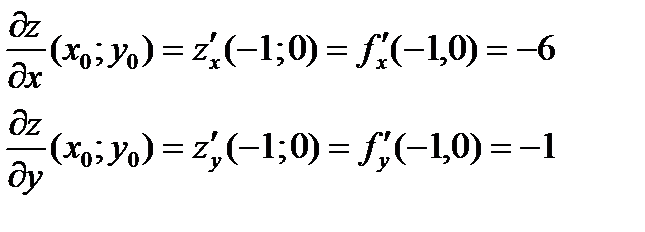
Используя уравнение касательной плоскости

 ,

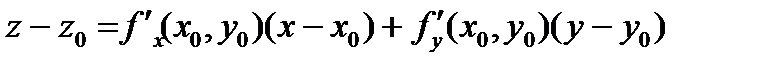получаем .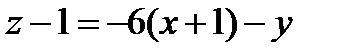

Следовательно, касательная плоскость имеет уравнение: .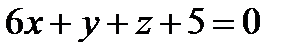

Уравнение нормали ищем в виде:

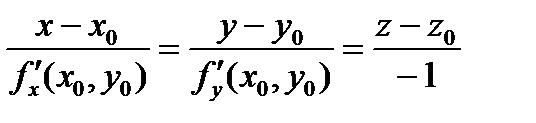
Получим 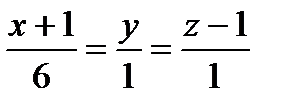    - уравнение нормали.

Задача 7.  С помощью полного дифференциала найти приближенное значение функции 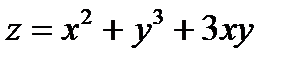в точке 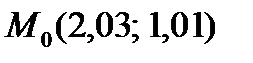с точностью до двух знаков после запятой.

Решение.     Приближенное значение функции в заданной точке находится по формуле:

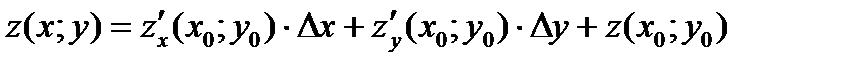
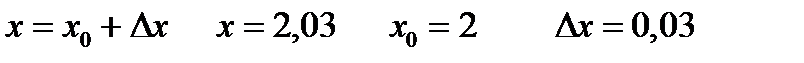
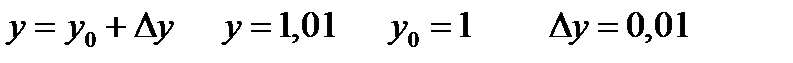
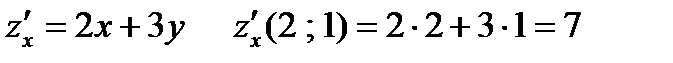
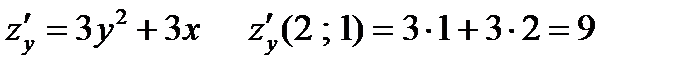
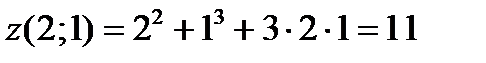
Приближенное значение функции 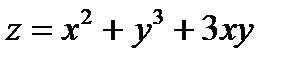в точке :


⇐ Предыдущая1234Следующая ⇒
  

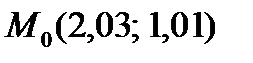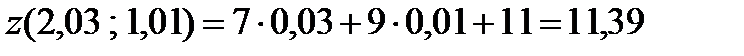
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.