
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Теоретические сведения.
Теоретические сведения.
Функция 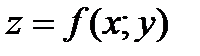 называется непрерывной в т.
называется непрерывной в т. 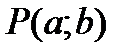 , если
, если 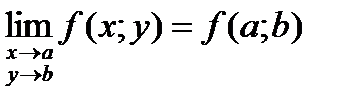 . Функция, непрерывная во всех точках некоторой области, называется непрерывной в этой области.
. Функция, непрерывная во всех точках некоторой области, называется непрерывной в этой области.
Линией уровня функции 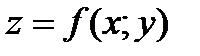 называется линия
называется линия 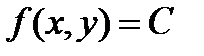 на плоскости
на плоскости 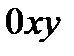 , в точках которой функция принимает одно и тоже значение
, в точках которой функция принимает одно и тоже значение 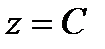 .
.
Частной производной от функции 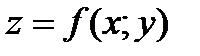 по независимой переменной
по независимой переменной 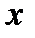 называется конечный предел:
называется конечный предел:
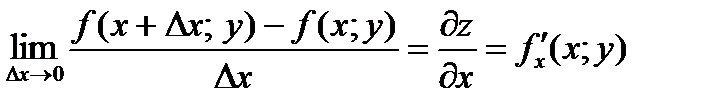 .
.
Аналогично определяется частная производная функции 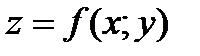 по переменной
по переменной  .
.
Полный дифференциал функции 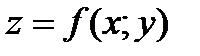 находится по формуле:
находится по формуле:
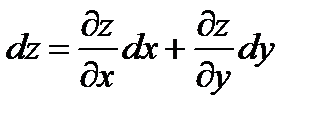 .
.
Частными производными второго порядка от функции 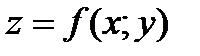 называются частные производные от ее частных производных первого порядка:
называются частные производные от ее частных производных первого порядка:
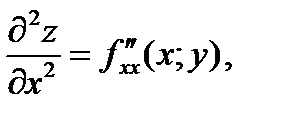

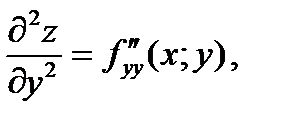

Функция  от переменных
от переменных 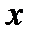 и
и 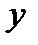 является неявной, если она задается уравнением
является неявной, если она задается уравнением 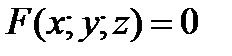 , неразрешенным относительно
, неразрешенным относительно 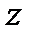 .
.
Частные производные функции двух переменных 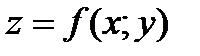 , заданной неявно с помощью уравнения
, заданной неявно с помощью уравнения 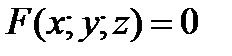 , находятся по формулам:
, находятся по формулам:
 ,
, 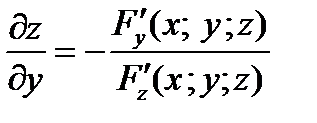 .
.
Градиентом функции 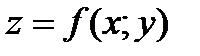 в точке
в точке 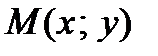 называется вектор с началом в точке
называется вектор с началом в точке 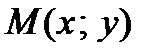 , имеющий своими координатами частные производные функции
, имеющий своими координатами частные производные функции 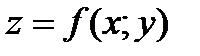 :
:
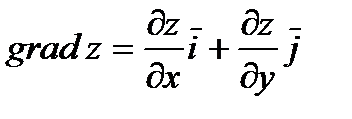 ,
,
где 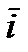 и
и  - взаимноперпендикулярные векторы единичной длины, задающие направление координатных осей Ох и Оу соответственно.
- взаимноперпендикулярные векторы единичной длины, задающие направление координатных осей Ох и Оу соответственно.
Градиент указывает направление наибыстрейшего роста функции в данной точке.
Касательной плоскостью к поверхности в т. М (точке касания) называется плоскость, в которой лежат все касательные прямые к различным кривым, проведенным на поверхности через эту точку.
Нормалью к поверхности называется прямая, перпендикулярная касательной плоскости.
Уравнение касательной плоскости к поверхности, заданной уравнением 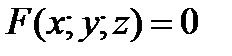 , с точкой касания
, с точкой касания 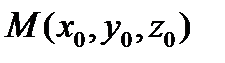 , записывается в виде:
, записывается в виде:
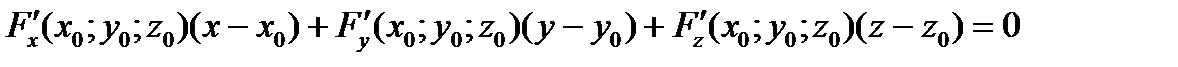
Уравнение нормали к поверхности, проходящей через точку касания 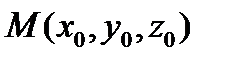 :
:
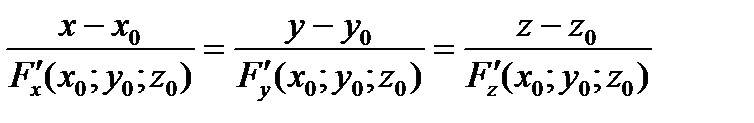
Если уравнение поверхности задано в виде 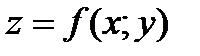 , то уравнение касательной плоскости:
, то уравнение касательной плоскости:
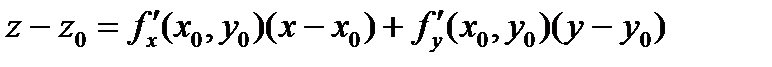 .
.
Уравнение нормали:
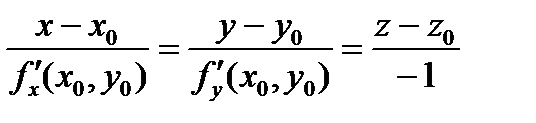 .
.
Минимумы и максимумы функции называются ее экстремумами.
Необходимое условие экстремума функции: если дифференцируемая функция 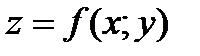 достигает экстремума в т.
достигает экстремума в т. 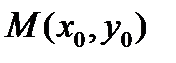 , то ее частные производные 1-го порядка в этой точке равны нулю:
, то ее частные производные 1-го порядка в этой точке равны нулю:
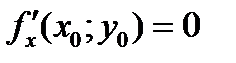 ,
, 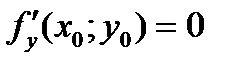
Точки, в которых частные производные функции 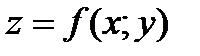 равны нулю, называются стационарными точками. Не всякая стационарная точка является точкой экстремума.
равны нулю, называются стационарными точками. Не всякая стационарная точка является точкой экстремума.
Достаточное условие экстремума. Пусть 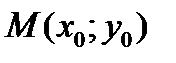 - стационарная точка функции
- стационарная точка функции 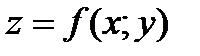 . Вычислим:
. Вычислим:
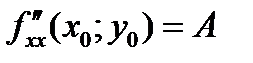 ,
, 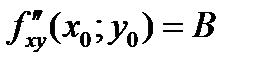 ,
, 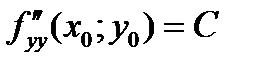
Обозначим: 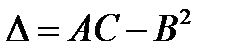 . Тогда:
. Тогда:
1. Если 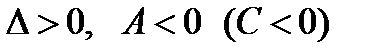 , то
, то 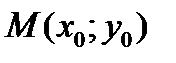 - точка максимума.
- точка максимума.
2. Если 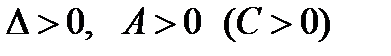 , то
, то 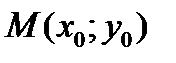 - точка минимума
- точка минимума
3. Если 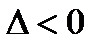 , то точка
, то точка 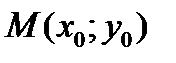 не является точкой экстремума.
не является точкой экстремума.
4. Если 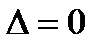 , то требуется дальнейшее исследование.
, то требуется дальнейшее исследование.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|