
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Имеет точку разрыва первого рода. Нет.
2)Имеет точку разрыва первого рода. Нет.
3)Ограничена. Да.
4)Принимает только положительные значения. Нет.
12. Дана функция 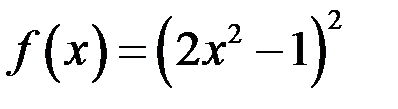 . Тогда верны следующие утверждения:
. Тогда верны следующие утверждения:
1)Функция убывает на промежутке . Да.
2)Функция имеет перегиб в точке . Да.
3)Значения функции в точке максимума равно . Нет.
4)Функция выпукла вниз на промежутке . Да.
Часть 2. В каждом следующем задании предлагаются несколько утверждений. Необходимо выбрать верное утверждение из предлагаемого набора альтернатив.
13.Корнями уравнения 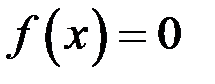 являются числа
являются числа 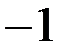 и
и 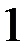 . Тогда корнями уравнения
. Тогда корнями уравнения 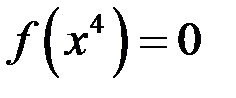 являются числа…
являются числа…
А)  и и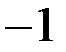
| *Б) 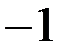 и и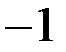
|
В) 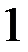 и и
| Г) 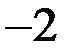 и и
|
14.Касательной к графику функции 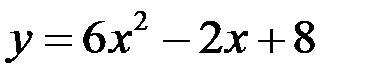 является прямая:
является прямая:
*А) 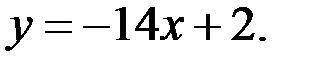
| Б) 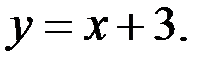
|
В) 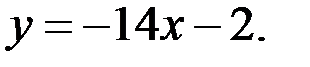
| Г) 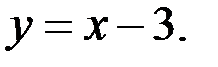
|
15.Касательной к графику функции 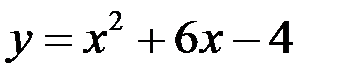 является прямая:
является прямая:
*А) 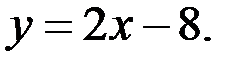
| Б) 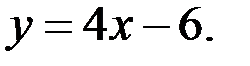
|
В) 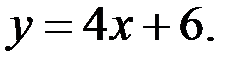
| Г) 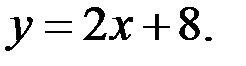
|
16.Касательной к графику функции 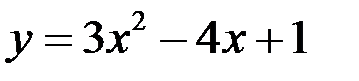 является прямая:
является прямая:
А) 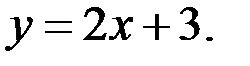
| Б) 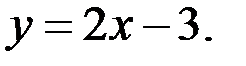
|
В) 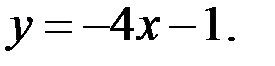
| *Г) 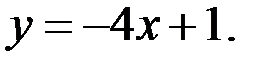
|
17.Дана функция 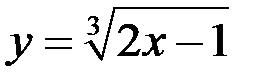 . Пусть
. Пусть 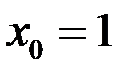 .
.
1)Тогда при 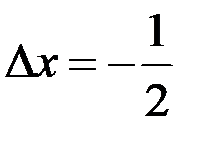 отношение
отношение 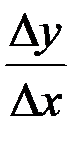 равно …
равно …
А) 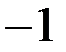
| *Б) 
| В) 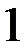
| Г) 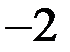
|
2)Значение выражения
А) 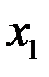
| Б) 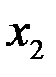
| В) 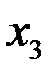
| *Г) 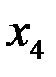
|
3)Значение дифференциала функции в точке 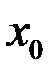 при
при 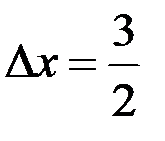 равно:
равно:
*А) 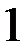
| Б) 
| В) 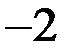
| *Г) 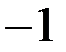
|
18.Пусть задана парабола 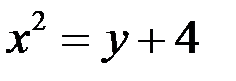 . Наибольшее число, раз параболу пересекает окружность …
. Наибольшее число, раз параболу пересекает окружность …
А) 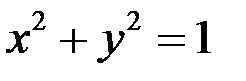
| Б) 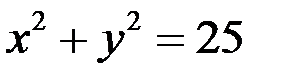
|
В) 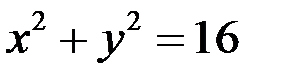
| *Г) 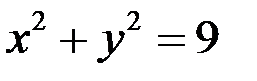
|
19.Пусть функция 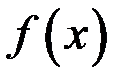 определена и непрерывна на отрезке
определена и непрерывна на отрезке 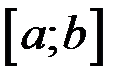 . Тогда всегда ложным является утверждение: …
. Тогда всегда ложным является утверждение: …
А) наибольшее и наименьшее значение функции 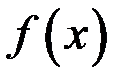 на отрезке
на отрезке 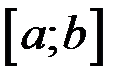 совпадают;
совпадают;
Б)наибольшеезначение функции 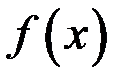 достигается в двух различных точках отрезка
достигается в двух различных точках отрезка 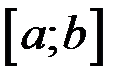 ;
;
В) ни наибольшее, ни наименьшее значение функции 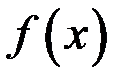 не достигаются во внутренних точках отрезка
не достигаются во внутренних точках отрезка 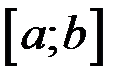 ;
;
*Г)функция 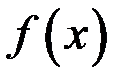 не принимает значение, равное среднему арифметическому наибольшего и наименьшего значений функции.
не принимает значение, равное среднему арифметическому наибольшего и наименьшего значений функции.
20.Пусть функция 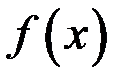 определена и непрерывна на отрезке
определена и непрерывна на отрезке 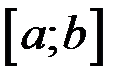 . Тогда верно утверждение: …
. Тогда верно утверждение: …
*А)наибольшее и наименьшее значение 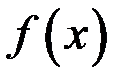 на отрезке
на отрезке 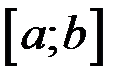 могут совпадать;
могут совпадать;
Б)наибольшее и наименьшее значения 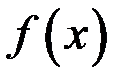 всегда достигаются во внутренних точках отрезка
всегда достигаются во внутренних точках отрезка 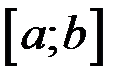 ;
;
В) наибольшее значение функции 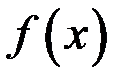 не может достигаться в двух различных точках отрезка
не может достигаться в двух различных точках отрезка 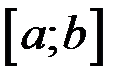 ;
;
Г)функция не может принимать значение, равное среднему арифметическому наибольшего и наименьшего своих значений на отрезке 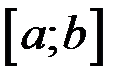 .
.
21..Пусть 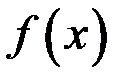 имеет непрерывную вторую производную и
имеет непрерывную вторую производную и 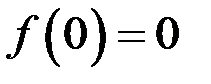 ,
, 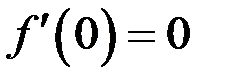 ,
, 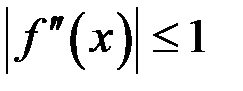 при всех
при всех 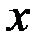 , тогда при всех
, тогда при всех 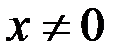 справедливо неравенство …
справедливо неравенство …
А) 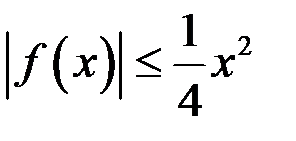
| *Б) 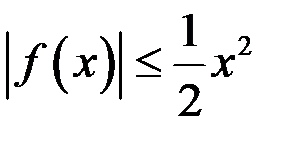
|
В) 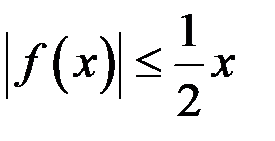
| Г) 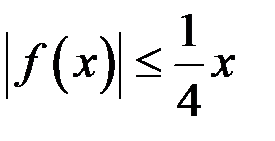
|
22.Пусть 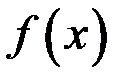 и
и 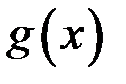 дважды дифференцируемая функция на всей оси. Тогда если
дважды дифференцируемая функция на всей оси. Тогда если 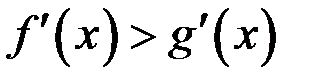 для всех
для всех 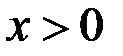 , то для всех
, то для всех 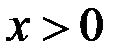 справедливо неравенство…
справедливо неравенство…
А) 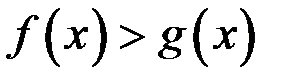
| Б) 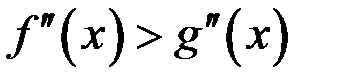
|
*В) 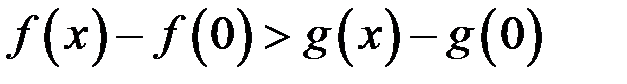
| Г) 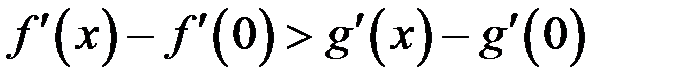
|
Часть 3. На каждое из заданий этой части Вы можете дать ответ в виде положительного или отрицательного числа.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|