
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Твердження. Типи практичних завдань
Твердження
1. Властивості і фізична інтерпретація криволінійних і поверхневих інтегралів.
2. Три інтегральні теореми: Гріна, Остроградського–Гаусса, Стокса. (З доведенням).
3. Умови незалежності криволінійного інтеграла від шляху інтегрування. (З доведенням). Інтегрування повних диференціалів.
4. Теорема про похідну в напрямі (з доведенням).
5. Теорема про збереження інтенсивності векторної трубки. (З доведенням).
6. Три інтегральні теореми: Гріна, Остроградського–Гаусса, Стокса. (З доведенням).
7. Теорема Гельмгольца.
8. Операції теорії поля в КОСК. *
Типи практичних завдань
1. 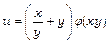 , де
, де 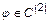 . Знайти
. Знайти 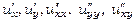 ,
, 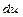 ,
, 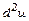 .
.
2. Функція 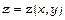 неявно задана рівнянням
неявно задана рівнянням 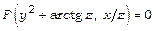 . Знайти
. Знайти  .
.
3. 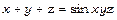 .Знайти
.Знайти 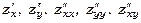 ,
, 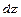 ,
, 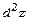 .
.
4.Написати три доданки формули Тейлора з залишковим членом у формі Лагранжа для функції
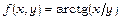 в точці
в точці 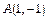 .
.
5.Знайти похідну функції 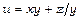 в точці
в точці 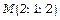 у напрямі градієнта функції
у напрямі градієнта функції 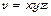 в цій точці.
в цій точці.
6.Знайти 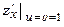 ,
, 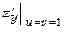 , якщо
, якщо 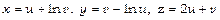 .
.
7. Знайти якобіан відображення  , де
, де 
8.Перетворити рівняння 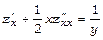 , якщо
, якщо 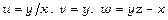 ;
; 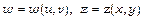 .
.
9. Дослідити на внутрішній локальний екстремум функцію 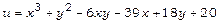 .
.
10.Знайти найбільше значення функції 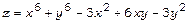 на множині
на множині
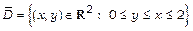 .
.
11.Дослідити на умовний екстремум функцію 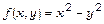 , якщо
, якщо 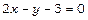 .
.
12. Змінити порядок інтегрування в інтегралі 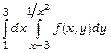 .
.
13. Перейшовши до полярних координат, обчислити подвійний інтеграл:
а) 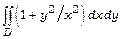 , якщо
, якщо 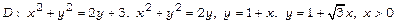 ;
;
б) 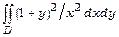 , якщо
, якщо 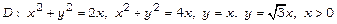 ;
;
в) 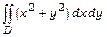 , якщо
, якщо  .
.
14. Знайти масу, статичні моменти і моменти інерції фігури 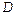 густини
густини 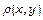 :
:
а) 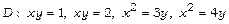 ,
, 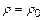 ; б)
; б) 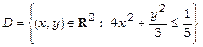
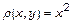 .
.
15. Звівши потрійний інтеграл до повторного двома способами, обчислити об’єм тіла
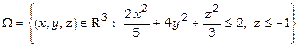 .
.
16. Знайти об’єм тіла, обмеженого поверхнею:
а) 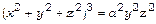 ; б)
; б) 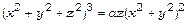 ;
;
в) 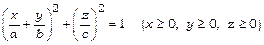 .
.
17. Знайти масу тіла 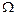 густини
густини 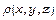 :
:
а)  ,
, 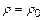 ; б)
; б) 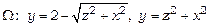 ,
, 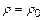 ;
;
в) 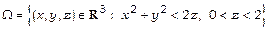 ,
, 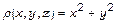 .
.
18. Знайти статичний момент  тіла
тіла 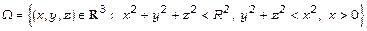 .
.
19. Знайти масу кривої 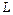 лінійної густини
лінійної густини 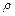 , якщо
, якщо
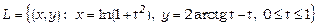 ,
, 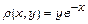 ,
, 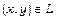 .
.
20. Обчислити координати центру мас однорідної поверхні 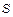 , якщо
, якщо
 .
.
21. Знайти роботу вектора 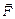 уздовж кривої
уздовж кривої 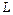 , якщо
, якщо 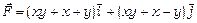 ,
,
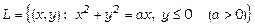 від точки
від точки 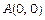 до точки
до точки 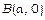 .
.
22. Обчислити потік векторного поля 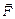 через ліву сторону поверхні
через ліву сторону поверхні 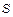 , якщо
, якщо
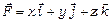 ,
, 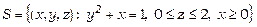 .
.
23.Перевірити, що  є повним диференціалом деякої функції
є повним диференціалом деякої функції 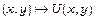 , якщо
, якщо
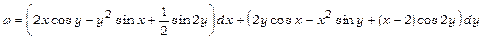 .
.
Знайти 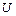 та обчислити
та обчислити 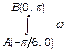 .
.
24. Використовуючи формулу Гріна, обчислити 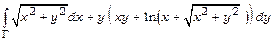 ,
,
де 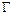 –– межа області
–– межа області  .
.
25. Застосовуючи формулу Гаусса–Остроградського, знайти потік вектора 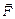 через внутрішню сторону поверхні
через внутрішню сторону поверхні 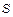 , якщо
, якщо
 ,
, 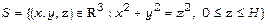 .
.
26. Використовуючи формулу Стокса, знайти циркуляцію вектора 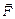 уздовж кривої
уздовж кривої 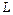 при напрямі обходу проти годинникової стрілки з боку додатної півосі
при напрямі обходу проти годинникової стрілки з боку додатної півосі 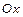 , якщо
, якщо
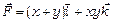 ,
,  .
.
27.Довести: а) 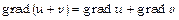 ; б)
; б)  ; в)
; в) 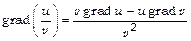 ;
;
г) 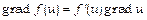 ; д)
; д) 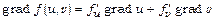 .
.
28.Обчислити: а)  ,
,  –– сталий вектор;
–– сталий вектор;
б) 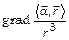 ; в)
; в)  ; г)
; г) 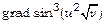 .
.
29.Знайти похідну скалярного поля  в точці
в точці 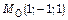 в напрямі від точки
в напрямі від точки 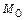 до точки
до точки 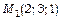 .
.
30.Обчислити: а) 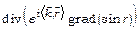 ; б)
; б) 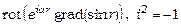 ,
,  –– сталий вектор.
–– сталий вектор.
31.Довести соленоїдність векторного поля 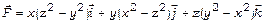 і знайти його векторний потенціал
і знайти його векторний потенціал 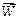 .
.
32.Довести потенціальність векторного поля 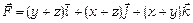 і знайти його потенціал
і знайти його потенціал 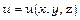 .
.
33. Обчислити: а) 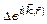 ; б)
; б) 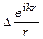 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|