
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Доказательство: Необходимо определить новый базис так, что при . Будем искать в виде
Доказательство: Необходимо определить новый базис так, что при . Будем искать в виде
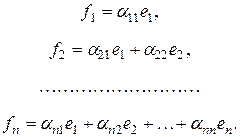
| (6) |
Коэффициенты  можно было бы найти из условия
можно было бы найти из условия 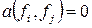 при
при 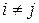 . Однако это привело бы к решению уравнений второго порядка на
. Однако это привело бы к решению уравнений второго порядка на  . Поступим иначе.
. Поступим иначе.
Если 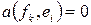 , для
, для 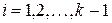 , то
, то 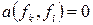 , для
, для 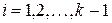 . Действительно, подставляя вместо
. Действительно, подставляя вместо 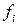 выражение
выражение  , получаем
, получаем 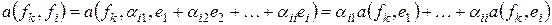
 если
если 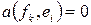 ,
, 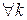 и
и 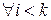 , то
, то 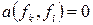
 в силу симметрии билинейных форм
в силу симметрии билинейных форм 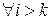 . Т. о., задача свелась к следующей: определить
. Т. о., задача свелась к следующей: определить 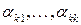 так, что
так, что 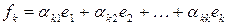 удовлетворяли условиям
удовлетворяли условиям
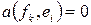 , для , для 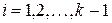 . .
| (7) |
Этими условиями 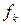 определяются с точностью до постоянного множителя. Зафиксируем этот множитель условием
определяются с точностью до постоянного множителя. Зафиксируем этот множитель условием
 . .
| (8) |
Сейчас увидим, что требования (7), (8) определяют вектор 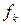 однозначно. Действительно, подставляя в (7), (8) выражение для
однозначно. Действительно, подставляя в (7), (8) выражение для 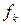 , имеем:
, имеем:
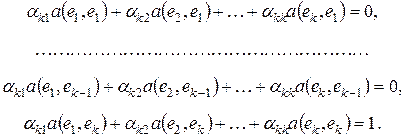 . .
| (9) |
По условию (5) определитель  этой системы линейных уравнений отличен от нуля
этой системы линейных уравнений отличен от нуля  по теореме Крамера решение $!.
по теореме Крамера решение $!.
Теперь найдем коэффициенты 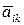 квадратичной формы в базисе
квадратичной формы в базисе 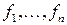 . Так как
. Так как 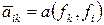 , то по построению
, то по построению 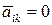 при
при  .
.
Вычислим 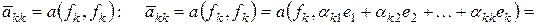 |в силу (7), (8)|=
|в силу (7), (8)|= 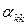 . По правилу Крамера, из (9)
. По правилу Крамера, из (9) 
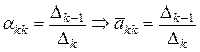 , что и требовалось доказать. ■
, что и требовалось доказать. ■
Замечание. Приведенный выбор базиса не единственный.
Пример. Привести к диагональному виду форму  , данную в базисе
, данную в базисе 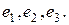
Здесь
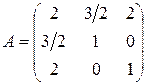 , и
, и  , т.е. не обращаются в нуль миноры из условия теоремы. Пусть
, т.е. не обращаются в нуль миноры из условия теоремы. Пусть
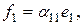
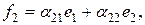
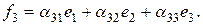 В силу теоремы о поляризации соответствующая билинейная форма имеет вид
В силу теоремы о поляризации соответствующая билинейная форма имеет вид

из 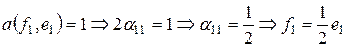 . Для
. Для 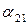 и
и 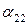 имеем уравнения
имеем уравнения  и
и 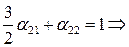

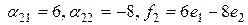 .
.
Наконец, для 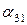 ,
, 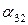 и
и 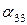 имеем систему уравнений:
имеем систему уравнений:
 т.е.
т.е. 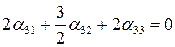 ,
, 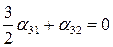 ,
, 
 ,
, 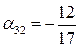 ,
, 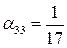 , т.е.
, т.е. 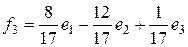 .
.
В этом базисе квадратичная форма имеет вид 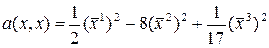 .
.
4°. Закон инерции квадратичных форм.
Как было показано ранее, число отличных от нуля коэффициентов в каноническом виде квадратичной формы не зависит от вида преобразования, с помощью которого 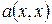 приводится к каноническому виду. В действительности, не меняется число положительных и отрицательных коэффициентов. Это свойство называется законом инерции квадратичных форм. А именно справедливо утверждение.
приводится к каноническому виду. В действительности, не меняется число положительных и отрицательных коэффициентов. Это свойство называется законом инерции квадратичных форм. А именно справедливо утверждение.
Теорема 4(закон инерции квадратичных форм). Число слагаемых с положительными (отрицательными) коэффициентами в каноническом виде квадратичной формы не зависит от способа приведения формы к этому виду.
Доказательство. Пусть форма 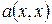 с помощью некоторого преобразования координат
с помощью некоторого преобразования координат 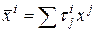 приводится к виду
приводится к виду
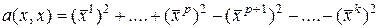 ,
,
а с помощью другого преобразования того же вида – к
 .
.
Для доказательства теоремы надо показать, что 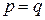 .
.
От противного. Предположим, что 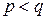 . Покажем, что в этом случае существует ненулевой вектор
. Покажем, что в этом случае существует ненулевой вектор 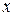 : в новых координатах
: в новых координатах 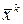 и
и 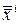 , координаты
, координаты  и
и 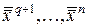 равны нулю, т.е.
равны нулю, т.е. 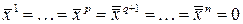
Каждое из этих уравнений имеет вид:
 ,
,
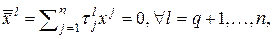 .
.
с известными 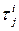 . Так как
. Так как 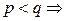 уравнений меньше, чем
уравнений меньше, чем 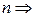 эти уравнения имеют ненулевое решение
эти уравнения имеют ненулевое решение 
 в силу равенства
в силу равенства 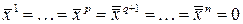
 в новых переменных
в новых переменных 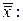
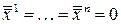 , т.е.
, т.е. 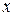 – нулевой вектор, что противоречит тому, что
– нулевой вектор, что противоречит тому, что 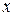 – ненулевой
– ненулевой  предположение
предположение 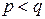 – неверно
– неверно 
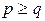 . В силу симметричности законов приведения
. В силу симметричности законов приведения 
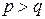 – неверно
– неверно 
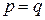 . Что и требовалось доказать. ■
. Что и требовалось доказать. ■
5°. Классификация квадратичных форм.
Определение 5. Индексом инерции квадратичной формы называется число отличных от нуля коэффициентов канонического вида (т.е. ранг формы), положительным (отрицательным) индексом – число положительных (отрицательных) коэффициентов.
Очевидно, что сумма положительных и отрицательных индексов инерции равна индексу инерции.
Обозначим  – индекс инерции, положительный и отрицательный индексы соответственно,
– индекс инерции, положительный и отрицательный индексы соответственно, 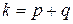 . Тогда квадратичная форма может быть приведена к виду
. Тогда квадратичная форма может быть приведена к виду 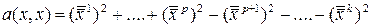 в некотором базисе
в некотором базисе 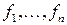 .
.
Утверждение 3: Для того, чтобы квадратичная форма 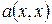 , заданная в
, заданная в 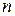 –мерном пространстве
–мерном пространстве 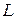 , была знакоопределенной, необходимо и достаточно, чтобы, либо
, была знакоопределенной, необходимо и достаточно, чтобы, либо  , либо
, либо 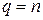 . Если
. Если  , то форма положительно определена, если
, то форма положительно определена, если 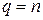 – отрицательно определена.
– отрицательно определена.
Доказательство: приведем для положительно определенной.
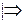
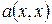 – положительно определена
– положительно определена  приводится к виду
приводится к виду 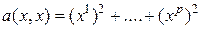 , если
, если 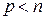 , то $
, то $ 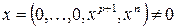 ,
,  .
.
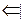 Пусть
Пусть 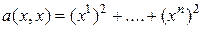

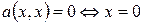 и
и 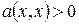 для
для 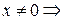
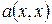 – положительно определена.
– положительно определена.
Утверждение 4: Форма 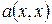 – знакопеременная
– знакопеременная  и положительный и отрицательный индексы отличны от нуля.
и положительный и отрицательный индексы отличны от нуля.
Доказательство:  квадратичная форма принимает и положительные и отрицательные значения
квадратичная форма принимает и положительные и отрицательные значения  в каноническом виде должны быть как положительные, так и отрицательные выражения
в каноническом виде должны быть как положительные, так и отрицательные выражения 
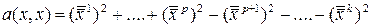 . .
| (10) |
 Если справедливо (10), то для
Если справедливо (10), то для 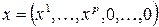 ,
, 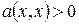 , а для
, а для 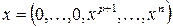 ,
, 
 (10) – канонический вид знакопеременной формы.
(10) – канонический вид знакопеременной формы.
Утверждение 5: Для того, чтобы 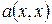 была квазизнакоопределенной, необходимо и достаточно, чтобы выполнялись соотношения либо
была квазизнакоопределенной, необходимо и достаточно, чтобы выполнялись соотношения либо 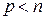 ,
, 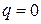 , либо
, либо 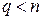 ,
, 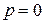 .
.
Доказательство: Аналогично п. 4
6°. Критерий Сильвестра знакоопределенности квадратичной формы.
(позволяет исследовать без приведения к каноническому виду)
Пусть 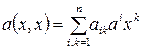 – квадратичная форма и
– квадратичная форма и 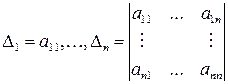 – угловые миноры.
– угловые миноры.
Теорема 5 (критерий Сильвестра). Для того, чтобы квадратичная форма 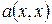 была положительно определена, необходимо и достаточно, чтобы были выполнены неравенства
была положительно определена, необходимо и достаточно, чтобы были выполнены неравенства 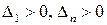 .
.
Для того чтобы, форма была отрицательно определенной, необходимо и достаточно, чтобы знаки угловых миноров чередовались, причем D1<0
Доказательство: 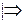 Докажем в начале, что из условия знакоопределенности следует, что
Докажем в начале, что из условия знакоопределенности следует, что 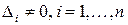
Ä пусть 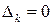 . Рассмотрим систему ЛОУ
. Рассмотрим систему ЛОУ
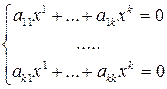 , то определитель
, то определитель 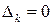
 система имеет нетривиальное решение. Пусть
система имеет нетривиальное решение. Пусть 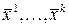 – такое решение. Умножая первое уравнение на
– такое решение. Умножая первое уравнение на 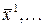
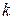 –е на
–е на 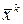 и складывая, получим :
и складывая, получим : 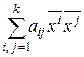 =0, т.е. получили, что квадратичная форма на ненулевом векторе
=0, т.е. получили, что квадратичная форма на ненулевом векторе 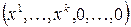 обращается в нуль. Это противоречит знакоопределенности
обращается в нуль. Это противоречит знакоопределенности 
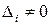 ,
, 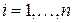 . Поэтому можно применить теорему Якоби (теорема 3) и воспользоваться формулой для коэффициентов
. Поэтому можно применить теорему Якоби (теорема 3) и воспользоваться формулой для коэффициентов 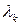 . Если
. Если 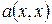 – положительно определена, то все
– положительно определена, то все 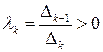 , так как
, так как 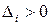 ,
, 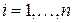 .
.
Если 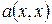 – отрицательно определенная форма, то
– отрицательно определенная форма, то 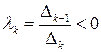

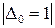

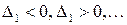 , т.е. знаки угловых миноров чередуются.
, т.е. знаки угловых миноров чередуются.
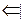 Пусть выполнены условия, что
Пусть выполнены условия, что 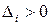 ,
, 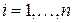
 можно воспользоваться методом Якоби
можно воспользоваться методом Якоби 

 форма положительно определена.
форма положительно определена.
Если знаки чередуются и 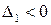 , то
, то 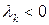
 форма отрицательно определена. Что и требовалось доказать. ■
форма отрицательно определена. Что и требовалось доказать. ■
Замечание:Отрицательный индекс инерции равен числу перемен знаков в последовательности определителей 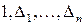 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|