
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Квадратичные формы
§6. Квадратичные формы
1°. Определение. Теорема о поляризации.
Определение 1. Пусть 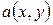 – симметрическая билинейная форма. Функция
– симметрическая билинейная форма. Функция 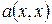 , которая получается из
, которая получается из 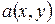 , если положить
, если положить 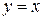 , называется квадратичной формой.
, называется квадратичной формой.
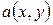 называется билинейной формой, полярной к квадратичной форме
называется билинейной формой, полярной к квадратичной форме 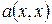 . Из симметричности
. Из симметричности 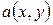 Þ
Þ
Теорема 1. Полярная форма 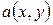 однозначно определяется своей квадратичной формой
однозначно определяется своей квадратичной формой 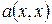 .
.
Доказательство. Из определения билинейной формы следует
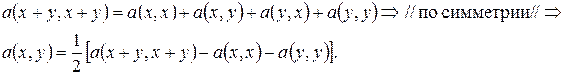
Справа стоят квадратичные формы Þ билинейная форма 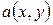 определяется своей квадратичной формой. ■
определяется своей квадратичной формой. ■
Матрица симметричной билинейной формы 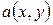 называется матрицей, соответствующей квадратичной форме
называется матрицей, соответствующей квадратичной форме 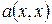 . Так как
. Так как
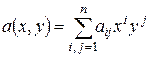
в данном фиксированном базисе, где  , то всякая квадратичная форма
, то всякая квадратичная форма 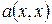 при заданном базисе выражается формулой:
при заданном базисе выражается формулой:
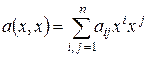 , (1)
, (1)
или в матричном виде,
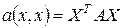 . (1¢)
. (1¢)
Правая часть (1) – однородный многочлен второй степени относительно  .Он содержит подобные члены в силу
.Он содержит подобные члены в силу 
 Þ после приведения подобных, имеем
Þ после приведения подобных, имеем
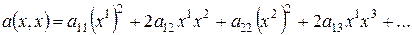 .
.
Еще два важных определения.
Определение 2. Квадратичная форма 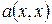 называется
называется
1) положительно (отрицательно) определенной, если 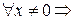

(такие формы называются знакоопределенными);
2) знакопеременной, если 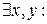
 .
.
3) квазизнакоопределенной, если 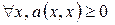 или
или 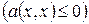 , но
, но 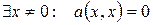 .
.
Далее будут указаны признаки, по которым форму можно отнести к каждому из классов.
Пример: 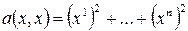 – положительно определенная.
– положительно определенная.
Определение 3. Ранг матрицы 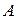 квадратичной формы
квадратичной формы 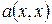 называется рангом квадратичной формы.
называется рангом квадратичной формы.
Если 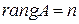 , то форма называется невырожденной, если
, то форма называется невырожденной, если 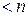 – то вырожденной.
– то вырожденной.
Далее нам понадобятся следующие две леммы о рангах матрицы.
Пусть 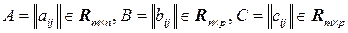 и
и 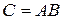 .
.
Лемма 1. Ранг произведения матриц не больше ранга любого из сомножителей, т.е.
 , (2)
, (2)
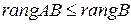 . (3)
. (3)
Доказательство. Докажем равенство (3). В начале тривиальные случаи:
1) если 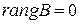 , то
, то 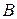 – нулевая
– нулевая 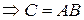 – нулевая
– нулевая 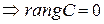 , т.е. (3) доказано.
, т.е. (3) доказано.
2) если  (число столбцов), то также очевидно, так как
(число столбцов), то также очевидно, так как 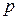 – число столбцов в
– число столбцов в 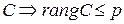 .
.
Далее пусть 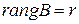 и
и 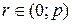 . Тогда
. Тогда 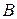 имеет
имеет  базисных столбцов и хотя бы один столбец не принадлежащий этой системе. Пусть
базисных столбцов и хотя бы один столбец не принадлежащий этой системе. Пусть  базисных столбцов – это первые столбцы. Тогда
базисных столбцов – это первые столбцы. Тогда  –ый столбец,
–ый столбец, 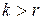 , выражается через них по теореме о базисном миноре:
, выражается через них по теореме о базисном миноре:
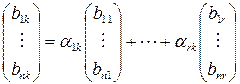 , т.е.
, т.е. 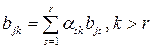 .
.
По определению произведения матриц имеем: 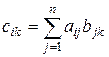 . Тогда
. Тогда 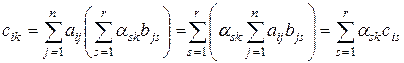 , т.е. в матрице
, т.е. в матрице  столбец с номером
столбец с номером 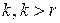 , также выражается через ее первые
, также выражается через ее первые  столбцов:
столбцов:
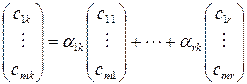 .
.
Значит, ранг столбцов матрицы 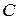 не больше
не больше  , т.е.
, т.е. 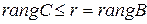 , т.е. (3) доказано.
, т.е. (3) доказано.
Для доказательства (2) перейдем к транспонированным матрицам: 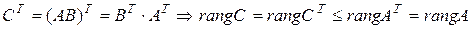 . ■
. ■
Замечание: Из Леммы 1 не следует, что первые  столбцов матрицы
столбцов матрицы 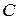 линейно независимы.
линейно независимы.
Лемма 2. Пусть  и
и 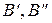 – невырожденные. Тогда
– невырожденные. Тогда 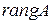 не изменяется при умножении на
не изменяется при умножении на  и на
и на 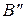 , т.е.
, т.е.
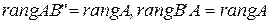 .
.
Доказательство. Пусть  (по Лемме 1). Но
(по Лемме 1). Но 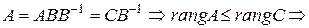 ч.т.д. ■
ч.т.д. ■
2°. Метод Лагранжа приведения квадратичной формы к каноническому виду.
Очевидно, что выражение (1) квадратичной формы через координаты вектора  зависит от выбора базиса в линейном пространстве. Оказывается, выбирая базис определенным образом, можно привести квадратичную форму к некоторому простейшему виду, а именно, справедлива
зависит от выбора базиса в линейном пространстве. Оказывается, выбирая базис определенным образом, можно привести квадратичную форму к некоторому простейшему виду, а именно, справедлива
Теорема 1. Для каждой квадратичной формы 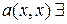 базис, в котором
базис, в котором
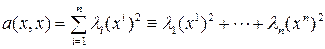 , (4)
, (4)
т.е. матрица квадратичной формы является диагональной.
Доказательство. По индукции по числу переменных.
1) При 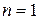 в произвольном базисе квадратичная форма имеет диагональный вид.
в произвольном базисе квадратичная форма имеет диагональный вид.
2) Пусть утверждение справедливо для квадратичной формы от 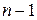 переменной и докажем для
переменной и докажем для 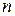 переменных. Пусть в произвольном базисе
переменных. Пусть в произвольном базисе
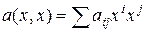 .
.
Если все 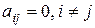 , то матрица диагональная. Далее будем рассматривать случай, когда хотя бы одно
, то матрица диагональная. Далее будем рассматривать случай, когда хотя бы одно 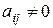 .
.
Рассмотрим два случая.
1) Все 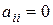 . Тогда перенумерованием переменных можно добиться, что
. Тогда перенумерованием переменных можно добиться, что 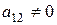 , т.е. имеется слагаемое
, т.е. имеется слагаемое  . Заменим координаты
. Заменим координаты 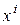 по формуле:
по формуле:
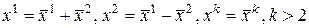 .
.
Этой замене соответствует матрица  , причём с определитель
, причём с определитель 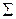 не равен 0. Т.е. это матрица
не равен 0. Т.е. это матрица 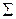 – матрица перехода к новому базису.
– матрица перехода к новому базису.
При этой замене член  перейдет в
перейдет в 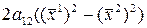 и, так как по предположению,
и, так как по предположению, 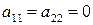 , то он ни с чем не может сократиться, и значит коэффициент при
, то он ни с чем не может сократиться, и значит коэффициент при 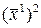 не равен 0.
не равен 0.
Таким образом, при необходимости делая перенумерование, всегда можем рассматривать случай:
2) 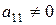 . Тогда в квадратичной форме
. Тогда в квадратичной форме  выделим все члены, содержащие
выделим все члены, содержащие 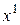 :
:
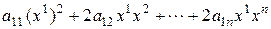 :
:
Дополним эту сумму до полного квадрата:
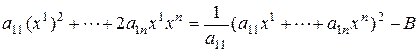 ,
,
где через 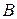 обозначены члены, содержащие лишь квадраты и попарные произведения членов
обозначены члены, содержащие лишь квадраты и попарные произведения членов 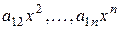 . Подстановка этого выражения в (1) дает
. Подстановка этого выражения в (1) дает
 ,
,
где 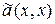 – квадратичная форма от
– квадратичная форма от 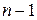 переменной
переменной 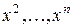 .
.
Согласно предположению индукции,  замена переменных
замена переменных
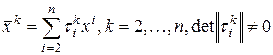 ,
,
согласно которой 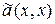 приводится к виду
приводится к виду
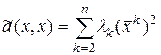 .
.
Положим  , и получим для
, и получим для 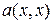 диагональный вид. Последняя замена имеет матрицу
диагональный вид. Последняя замена имеет матрицу 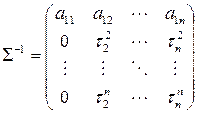 и
и 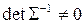 .
.
Обратная к ней матрица является матрицей перехода к искомому базису. ▄
Замечание 1: Способ приведения квадратичной формы к диагональному виду, данный в доказательстве, называется методом выделения квадратов.
Пример: 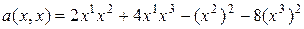
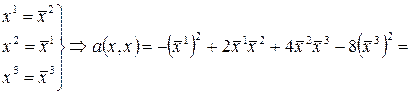
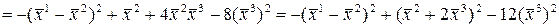 .
.
Определение 4. Диагональный вид квадратичной формы в вещественном пространстве называется каноническим, если коэффициенты 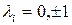 .
.
В комплексном пространстве вид канонический, если 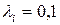 .
.
Базис, в котором квадратичная форма имеет канонический вид, называется каноническим. Он, обычно, определен неоднозначно.
Следствие (к Теореме 1). Для каждой квадратичной формы  базис, в котором она имеет канонический вид.
базис, в котором она имеет канонический вид.
Доказательство. Вначале приведем квадратичную форму к диагональному виду, а затем, если 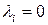 , то
, то 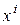 остаётся без изменения, если
остаётся без изменения, если 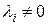 , то замена
, то замена 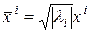 .
.
Очевидно, что после этого получается канонический вид и эта замена невырожденная. ■
Замечание 2 (о ранге квадратичной формы). После приведения квадратичной формы к диагональному виду переменные перенумеровывают так, что первые 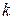 переменных имеют ненулевые
переменных имеют ненулевые  (первые
(первые 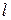 слагаемых имеют коэффициент 1, остальные (–1)) и далее 0:
слагаемых имеют коэффициент 1, остальные (–1)) и далее 0:
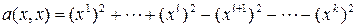 .
.
Ясно, что 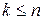 . Очевидно, что в силу Леммы 1и 2, при переходе к новому базису ранг
. Очевидно, что в силу Леммы 1и 2, при переходе к новому базису ранг  не меняется
не меняется  и значит, т.к. он для канонического вида равен
и значит, т.к. он для канонического вида равен 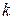 , то и в
, то и в 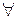 другом базисе равен
другом базисе равен 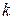 . Более того, при любом приведении к каноническому виду число отличных от нуля канонических коэффициентов одно и то же и равно рангу квадратичной формы.
. Более того, при любом приведении к каноническому виду число отличных от нуля канонических коэффициентов одно и то же и равно рангу квадратичной формы.
3°. Метод Якоби приведения к каноническому виду.
Дает формулы, выражающие искомый канонический базис 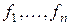 через исходный
через исходный  .
.
Теорема 3. Пусть в базисе 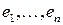 квадратичная форма имеет вид
квадратичная форма имеет вид 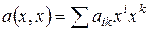 ,
, 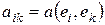 . Пусть определители
. Пусть определители
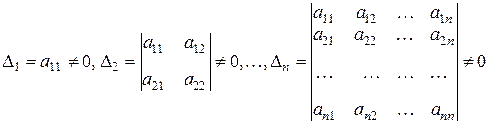 . .
| (5) |
Тогда существует базис  , в котором
, в котором 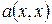 записывается в виде суммы квадратов следующим образом
записывается в виде суммы квадратов следующим образом  , где
, где 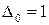 и
и 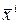 – координата вектора
– координата вектора 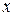 в базисе
в базисе 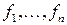 .
.
Дающийся в теореме способ приведения квадратичной формы к сумме квадратов называется методом Якоби.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|