sin(−x)=−sinx. п.3. Примеры

⇐ ПредыдущаяСтр 3 из 3

−1≤sinx≤1

Область значений y∈[−1;1]

3. Функция нечётная

sin(−x)=−sinx

4. Функция периодическая с периодом 2π

sin(x+2πk)=sinx,к∈Z.

5. Максимальные значения ymax=1 достигаются в точках

x=π/2+2πk , к∈Z.

Минимальные значения ymin=−1 достигаются в точках

x=−π/2+2πk, к∈Z.

Нули функции y₀=sinx₀=0 достигаются в точках x₀=πk, к∈Z.

6. Функция возрастает на отрезках

−π/2+2πk≤x≤π/2+2πk, к∈Z.

Функция убывает на отрезках

π/2+2πk≤x≤3π/2+2πk, к∈Z.

7. Функция непрерывна.

п.3. Примеры

Пример 1.Найдите наименьшее и наибольшее значение функции y=sinx на отрезке:

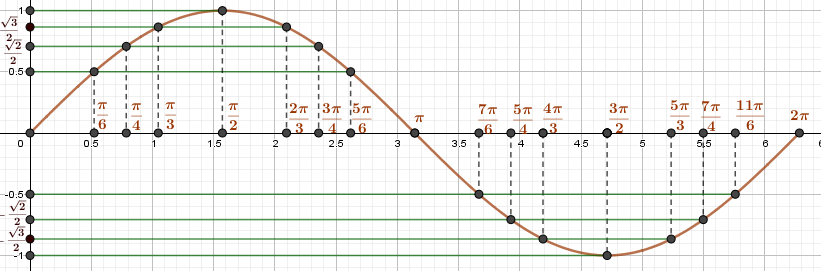
a) [π/6;3π/4] ymin=sin(π/6)=12, ymax=sin(π/2)=1б) [5π/6;5π/3]ymin=sin(3π/2)=−1,

ymax=sin(5π/6)=12

Пример 2. Постройте в одной системе координат графики функцийy=sinx, y=−sinx, y=2sinx, y=sinx+2

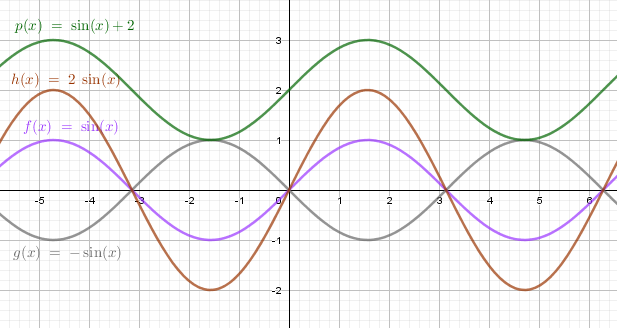
y=−sinx – отражение исходной функции y=sinx относительно оси OX. Область значений y∈[−1;1].
y=2sinx – исходная функция растягивается в 2 раза по оси OY. Область значений y∈[−2;2].
y=sinx+2 - исходная функция поднимается вверх на 2. Область значений y∈[1;3].

Пример 3. Постройте в одной системе координат графики функцийy=sinx, y=sin2x, y=sinx2

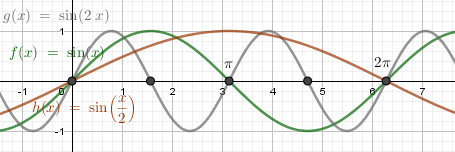
Амплитуда колебаний у всех трёх функций одинакова, область значений y∈[−1;1].
Множитель под синусом изменяет период колебаний.
y=sin2x - период уменьшается в 2 раза, полная волна укладывается в отрезок 0≤x≤π.
y=sinx2 - период увеличивается в 2 раза, полная волна укладывается в отрезок 0≤x≤4π.

⇐ Предыдущая 1 23