п.1. Развертка ординаты движения точки по числовой окружности в функцию от угла.

⇐ ПредыдущаяСтр 2 из 3Следующая ⇒

План

1. Развертка ординаты движения точки по числовой окружности в функцию от угла.

2. Свойства функции y=sinx:

Область определения,

Область значения,

Нули функции,

Промежутки возрастания, убывания функции,

Промежутки знакопостоянства,

Четность функции,

Монотонность функции,

Наименьшее и наибольшее значение функции.

3.Повторение:

- Какую функцию называют периодической?

- Что такое период?

- Какое число является главным периодом функции у = sin х?

п.1. Развертка ординаты движения точки по числовой окружности в функцию от угла.

При движении точки по числовой окружности её ордината является синусом соответствующего угла.

Рассмотрим, как изменяется синус, если точка описывает полный круг, и угол x изменяется в пределах: 0≤x≤2π и построим график y=sinx на этом отрезке.

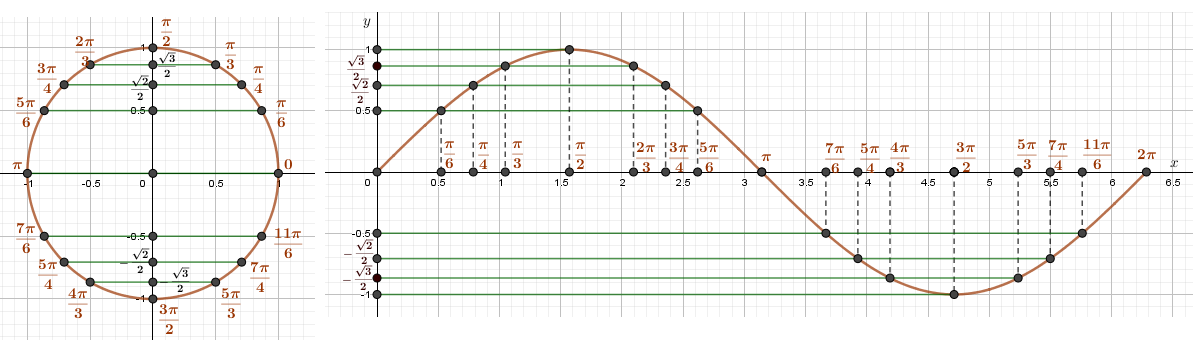
Если мы продолжим движение по окружности для углов x > 2π, кривая продолжится вправо; если будем обходить числовую окружность в отрицательном направлении (по часовой стрелке) для углов x<0, кривая продолжится влево.

В результате получаем график y=sinx для любого x∈R.

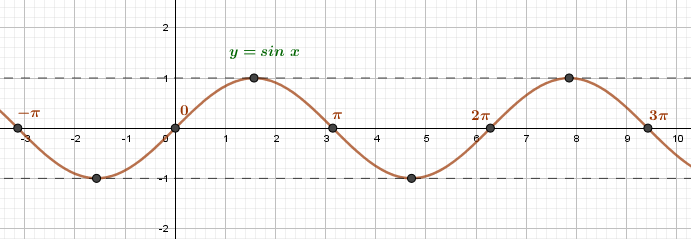
График y=sinx называют синусоидой.
Часть синусоиды для 0≤x≤2π называют волной синусоиды.
Часть синусоиды для 0≤x≤π называют полуволной или аркой синусоиды.

п.2. Свойства функции y=sinx⁡

1. Область определения x∈R - множество действительных чисел.

2. Функция ограничена сверху и снизу

⇐ Предыдущая 123 Следующая ⇒