Имеем разные плоскости: плоскость , плоскость . Известно, что они имеют общую точку М, точка М принадлежит плоскости и плоскости . (Рис. 5)

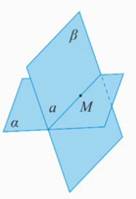
Рис. 5.

Отсюда вытекает, что существует прямая , которая проходит через точку М, которая одновременно принадлежит и плоскости a, и плоскости b. Вот в этом случае и говорят, что плоскости и пересекаются по прямой .

Записать:

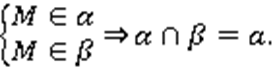
III. Закрепление изученного материала 1. Прочитать формулировки аксиом A1-А3.

2. Решаем задачи:

Задача 1(а,б) с. 7.

Ответ:
а) Точки Р и Е лежат в плоскости (ADB), а значит и прямая РЕ лежит в плоскости (ADB) (по A₁).

Аналогично МК лежит в плоскости (BDC).Точки В и D лежат одновременно в плоскостях (ADB) и (BDC), а значит прямая BD лежит в плоскостях (ADB) и (АВС).

Аналогично АВ лежит в плоскостях (ADB) и (АВС). Точки С и Е лежат одновременно в плоскостях ( АВС) и (DEC), а значит прямая СЕ лежит в этих же плоскостях.

б) Заметим, что точка С лежит на прямой DK и в плоскости (АВС), а следовательно, DK ∩(ABC) в точке С , так как точек пересечения более одной (прямая не лежит в плоскости),то это единственная точка.

Аналогично СЕ пересекается с плоскостью (ADB) в точке Е.

Задача 2(a) с. 7.

Ответ: а) В плоскости (DCC₁): D, С, С₁, К, М, R (см. 1).

В плоскости (BQC): В₁,В, Р, Q, C₁, М, С.

Подведение итогов

Мы познакомились с новым разделом геометрии - стереометрией, узнали новые аксиомы и использовали их при решении задач.
Домашнее задание

Повторить аксиомы планиметрии.

Выучить аксиомы А1-А3.

Прочитать пункт 1-2.

Задача 1(в, г), Задача 2 (б, д)

⇐ Предыдущая 1 23