
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Совместные и несовместные события. Противоположные события. Полная группа событий.
Конспект
Теория вероятностей. Что изучает эта наука (вернее раздел математики)? Все мы пользовались такими выражениями, как «вероятность дождя велика», «вероятность выигрыша в лотерею мала», «орёл и решка выпадают с вероятностью 50 на 50» и т.п. Но тогда сразу возникает вопрос, при чём здесь наука? Пожалуйста, прямо сейчас возьмите в руки монету и скажите, какой гранью она выпадет после броска? Сможем ответить на этот вопрос?…Совсем не похоже на теорию – скорее какое-то гадание….
И действительно, обывательское понимание вероятности больше смахивает на некое предсказание, часто с изрядной долей мистицизма и суеверий.
Мы с вами не можем угадать результат броска той же монеты в единичном эксперименте. Однако если одну и ту же монету в одинаковых условиях подбрасывать сотни и тысячи раз, то будет прослеживаться чёткая закономерность, описываемая вполне жёсткими законами.Знание этих закономерностей позволяют человеку уверенно чувствовать себя при встрече со случайными событиями. Подытожим:Теория вероятностей изучает вероятностные закономерности массовыходнородных случайных событий.
Рассмотрим основные понятия теории вероятности.
Теория вероятности, как и любой, раздел математики, оперирует определённым кругом понятий. Большинству понятий теории вероятностей даются определения, но некоторые принимаются за первичные, не определяемые, как в геометрии точка, прямая, плоскость. Первичным понятием теории вероятностей является событие. События являются результатом испытания. Например, подбрасывание монеты – испытание, а появление на ней “герба” – событие. Событие принято обозначать заглавными латинскими буквами: A,B,C,…События бывают достоверными, невозможными и случайными.
Достоверным называют событие, которое в результате испытания (осуществления определенных действий, определённого комплекса условий) обязательно произойдёт. Например, в условиях земного тяготения подброшенная монета непременно упадёт вниз.
Невозможным называют событие, которое заведомо не произойдёт в результате испытания. Пример невозможного события: в условиях земного тяготения подброшенная монета улетит вверх.
И, наконец, событие называется случайным, если в результате испытания оно может, как произойти, так и не произойти, при этом должен иметь место принципиальный критерий случайности: случайное событие – есть следствие случайных факторов, воздействие которых предугадать невозможно или крайне затруднительно. Другая важная характеристика событий – это их равновозможность. Два или большее количество событий называют равновозможными, если ни одно из них не является более возможным, чем другие. Например:
выпадение орла или решки при броске монеты;
выпадение 1, 2, 3, 4, 5 или 6 очков при броске игрального кубика; .
Могут ли быть те же события не равновозможными? Могут! Например, если у монеты или кубика смещён центр тяжести, то гораздо чаще будут выпадать вполне определённые грани.
Совместные и несовместные события. Противоположные события. Полная группа событий.
События называют несовместными, если в одном и том же испытании появление одного из событий исключает появление других событий. Простейшим примером несовместных событий является пара противоположных событий. Событие, противоположное данному, обычно обозначается той же латинской буквой с чёрточкой вверху. Например:
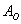 – в результате броска монеты выпадет орёл;
– в результате броска монеты выпадет орёл;
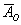 – в результате броска монеты выпадет решка.
– в результате броска монеты выпадет решка.
Совершено ясно, что в отдельно взятом испытании появление орла исключает появление решки (и наоборот), поэтому данные события и называются несовместными.
Противоположные события легко формулируются из соображений элементарной логики:
в результате броска игрального кубика выпадет 5 очков;
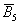 – в результате броска игрального кубика выпадет число очков, отличное от пяти.
– в результате броска игрального кубика выпадет число очков, отличное от пяти.
Либо пять, либо не пять – третьего не дано, т.е. события несовместны и противоположны.
Множество несовместных событий образуют полную группу событий, если в результате отдельно взятого испытания обязательно появится одно из этих событий. Очевидно, что любая пара противоположных событий (в частности, примеры выше) образует полную группу.
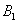 – в результате броска игрального кубика выпадет 1 очко;
– в результате броска игрального кубика выпадет 1 очко;
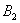 – … 2 очка;
– … 2 очка;
 – … 3 очка;
– … 3 очка;
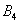 – … 4 очка;
– … 4 очка;
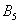 – … 5 очков;
– … 5 очков;
 – … 6 очков.
– … 6 очков.
События 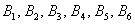 несовместны (поскольку появление какой-либо грани исключает одновременное появление других) и образуют полную группу (так как в результате испытания непременно появится одно из этих шести событий).
несовместны (поскольку появление какой-либо грани исключает одновременное появление других) и образуют полную группу (так как в результате испытания непременно появится одно из этих шести событий).
Ещё одно важное понятие, которое нам скоро потребуется – это элементарность исхода (события). Если совсем просто, то элементарное событие «нельзя разложить на другие события». Например, события 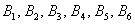 элементарны, но событие
элементарны, но событие 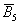 не является таковым, так как подразумевает выпадение 1, 2, 3, 4 или 6 очков (включает в себя 5 элементарных исходов).
не является таковым, так как подразумевает выпадение 1, 2, 3, 4 или 6 очков (включает в себя 5 элементарных исходов).
Совместные события менее значимы с точки зрения решения практических задач, но обходить их стороной не будем. События называются совместными, если в отдельно взятом испытании появление одного из них не исключает появление другого. Например:
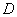 – завтра в 12.00 будет дождь;
– завтра в 12.00 будет дождь;
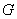 – завтра в 12.00 будет гроза;
– завтра в 12.00 будет гроза;
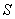 – завтра в 12.00 будет солнце.
– завтра в 12.00 будет солнце.
Ситуация, конечно, довольно редкая, но совместное появление всех трёх событий в принципе не исключено. Следует отметить, что перечисленные события совместны и попарно, т.е. может быть только ливень с грозой или грибной дождик, или погромыхает неподалёку на фоне ясного неба.
Независимымиявляются события, если вероятность наступления любого из них не зависит от появления/непоявления остальных событий рассматриваемого множества (во всех возможных комбинациях).
Итак, достоверное событие – это событие, наступающее при данных условиях со стопроцентной вероятностью (т.е. наступающее в 10 случаях из 10, в 100 случаях из 100 и т.д.). Невозможное событие – это событие, не наступающее при данных условиях никогда, событие с нулевой вероятностью.
Но, к сожалению (а может быть, и к счастью), не все в жизни так четко и ясно: это будет всегда (достоверное событие), этого не будет никогда (невозможное событие). Чаще всего мы сталкиваемся именно со случайными событиями, одни из которых более вероятны, другие менее вероятны. Обычные люди используют слова “более вероятно” или “менее вероятно”, как говорится, по наитию, опираясь на то, что называется здравым смыслом. Но очень часто такие оценки оказываются недостаточными, поскольку бывает важно знать, на сколько процентов вероятно случайное событие или во сколько раз одно случайное событие вероятнее другого. Иными словам, нужны точные количественные характеристики, нужно уметь охарактеризовать вероятность числом.
Первые шаги в этом направлении мы с вами уже сделали. Мы говорили, что вероятность наступления достоверного события характеризуется как стопроцентная, а вероятность наступления невозможного события – как нулевая. Учитывая, что 100% равно 1, люди договорились о следующем:
1) вероятность достоверного события считается равной 1;
2) вероятность невозможного события считается равной 0.
А как подсчитать вероятность случайного события? Ведь оно произошло случайно, значит, не подчиняется закономерностям, алгоритмам, формулам. Оказывается, и в мире случайного действуют определенные законы, позволяющие вычислять вероятности. Этим занимается раздел математики, который как мы уже сказали, и называется – теория вероятностей.
В практической жизни мы сталкиваемся с различными случайными событиями, причём они происходят с разной частотой: одни чаще, другие реже.
Вероятность события – это центральное понятие теории вероятностей. Существует несколько подходов к её определению:
Классическое определение вероятности;
Геометрическое определение вероятности;
Статистическое определение вероятности.
Мы с вами остановимся на классическом определении вероятностей, которое находит наиболее широкое применение в учебных заданиях.
Обозначения. Вероятность некоторого события 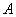 обозначается большой латинской буквой
обозначается большой латинской буквой 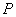 , а само событие берётся в скобки, выступая в роли своеобразного аргумента. Например:
, а само событие берётся в скобки, выступая в роли своеобразного аргумента. Например:
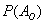 – вероятность того, что в результате броска монеты выпадет «орёл»;
– вероятность того, что в результате броска монеты выпадет «орёл»;
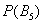 – вероятность того, что в результате броска игральной кости выпадет 5 очков;
– вероятность того, что в результате броска игральной кости выпадет 5 очков;
 – вероятность того, что в результате броска монеты выпадет «орёл»;
– вероятность того, что в результате броска монеты выпадет «орёл»;
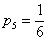 – вероятность того, что в результате броска игральной кости выпадет 5 очков;
– вероятность того, что в результате броска игральной кости выпадет 5 очков;
Классическое определение вероятности:
Вероятностью наступления события 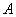 в некотором испытании называют отношение
в некотором испытании называют отношение 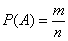 , где:
, где:
 – общее число всех равновозможных, элементарных исходов этого испытания, которые образуют полную группу событий;
– общее число всех равновозможных, элементарных исходов этого испытания, которые образуют полную группу событий;
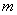 – количество элементарных исходов, благоприятствующих событию
– количество элементарных исходов, благоприятствующих событию 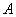 .
.
При броске монеты может выпасть либо орёл, либо решка – данные события образуют полную группу, таким образом, общее число исходов 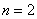 ; при этом, каждый из них элементарен и равновозможен. Событию
; при этом, каждый из них элементарен и равновозможен. Событию 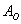 благоприятствует
благоприятствует 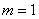 исход (выпадение орла). По классическому определению вероятностей:
исход (выпадение орла). По классическому определению вероятностей: 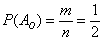 .
.
Принято использовать доли единицы, и, очевидно, что вероятность может изменяться в пределах 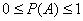 . При этом если
. При этом если 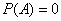 , то событие
, то событие 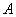 является невозможным, если
является невозможным, если 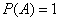 – достоверным, а если
– достоверным, а если 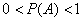 , то речь идёт о случайном событии.
, то речь идёт о случайном событии.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|