Проверка.. Ответ: х = 2. Проверка.. Ответ: х = 3.. Решение

⇐ ПредыдущаяСтр 3 из 4Следующая ⇒

Проверка.

Подставим в исходное уравнение х₁ = 2.

Получим: 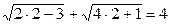, 1 + 3 = 4 (получили верное равенство).

Значит х₁ = 2 являетсякорнем исходного уравнения.

Подставим в исходное уравнение х₂ = 42.

Получим: 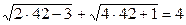, 9 + 13 ¹ 4.

Корень х₂ = 42исходному уравнению не удовлетворяет, следовательно, он является посторонним.

Ответ: х = 2

5.Решите уравнение .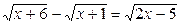

Решение

Возведем обе части уравнения в квадрат: .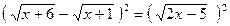

Получим х + 6 - 2 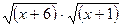+х+1= 2х - 5,

или х + 6 - 2 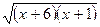+х+1= 2х – 5,

откуда 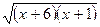= 6.

После возведения обеих частей этого уравнения в квадрат и приведения подобных членов получим х²+ 7х – 30 = 0.

Это уравнение имеет корни х₁ = -10, х₂ = 3.

Проверка.

Подставим в исходное уравнение х₁ = -10.

Получим: , .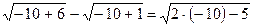

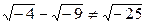Получили, что подкоренные выражения являются отрицательными числами, а квадратные корни из отрицательных чисел не имеют смысла.

Значит корень х₁ = -10является посторонним.

Подставим в исходное уравнение х₂ = 3.

Получим: 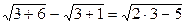, 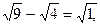3-2=1(получили верное равенство). Значит х₂ = 3 являетсякорнем исходного уравнения.

Ответ: х = 3.

6.Решите уравнение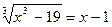

Решение

Возведем обе части уравнения в куб .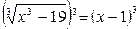

Получим: х³ – 19 = (х – 1)³,откуда х³ – 19 = х³– 3х² +3х – 1, 3х² – 3х - 18 = 0.

Это квадратное уравнение имеет корни х₁ = -2, х₂ = 3.

Так как в процессе решения данного уравнения были произведены равносильные преобразования, то проверку можно не проводить. Напоминаю, что при возведенииобеих частей уравнения в нечетную степень получается уравнение, равносильное исходному (посторонние корни не появляются).

Ответ: х1 = -2, х2 = 3.

⇐ Предыдущая 1 234 Следующая ⇒