РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ

РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ

СПРАВОЧНЫЙ МАТЕРИАЛ

1.Уравнения, в которых переменная содержится под знаком корня (радикала), называются иррациональными.

2.Решение иррациональных уравнений сводится к переходу от иррациональ - ного к рациональному уравнению путем возведения обеих частей уравнения в одну и ту же натуральную степень или замены переменной.

3. При возведении обеих частей уравнения в четную степень возможнопоявление посторонних корней. Поэтому при использовании указанного метода следует проверить все найденные корни подстановкой в исходное уравнение.

4. При возведенииобеих частей уравнения в нечетную степень получается уравнение, равносильное исходному (посторонние корни не появляются).

5.При решении иррациональных уравнений проверка не делается, если используются следующие утверждения:

5.1. уравнение вида 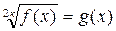где k Î N, равносильно системе

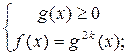
5.2. уравнение вида 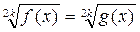, где kÎ N, равносильно системе

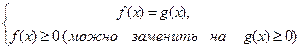
Примеры с решениями

1. Решите уравнение .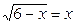

Решение. I вариант оформления.

Возведем обе части уравнения в квадрат: .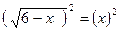

Получим уравнение 6 - х = х².

После переноса всех членов уравнения в одну часть получим квадратное уравнение: х² + х – 6 = 0.

Это уравнение имеет корни х₁ = -3, х₂ = 2.

Проверка. Если х₁ = -3,то 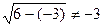. Корень х₁ = -3уравнению не удовлетворяет, следовательно, он является посторонним.

Если х₂ = 2,то второй корень удовлетворяет данному уравнению так как равенствоверное

12 3 4 Следующая ⇒