Ответ: х = 2.. Ответ: х = 2.. Ответ: х = 2. Решение. Решите данное уравнение самостоятельно,если в ходе вашего решения вы пришли к окончательному ответух=1. Вы на правильном пути. Можно двигаться дальше.

⇐ ПредыдущаяСтр 2 из 4Следующая ⇒

Ответ: х = 2.

II вариант оформления.

Уравнение 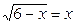равносильно системе

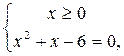
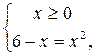
х₁ = -3посторонний корень так как не удовлетворяет условию х ³ 0

Ответ: х = 2.

2. Решите уравнение .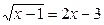

Решение

Возведем обе части уравнения в квадрат: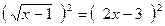

Получим: х – 1= 4х²– 12х + 9;после переноса всех членов в левую часть и приведения подобных членов имеем: 4х² – 13х + 10 = 0.

Это уравнение имеет корни: х₁ = 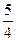и х₂ = 2.

Проверка. Если х₁ = 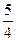,то 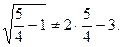Корень х₁ = 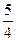уравнению не удовлетворяет, следовательно, он является посторонним.

Если х₂ = 2,то второй корень удовлетворяет данному уравнению так как равенство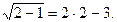верное.

Ответ: х = 2

3. Решите уравнение .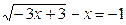

Решение

Прежде чем возводить данное уравнение в квадрат, преобразуем его (как говорят, «уединим корень (радикал)». Оставим корень в левой части, а х перенесем в правую часть уравнения с противоположным знаком.

Получим уравнение .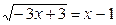

Задача сведена к предыдущей, см. пример 2.

Решите данное уравнение самостоятельно,если в ходе вашего решения вы пришли к окончательному ответух=1. Вы на правильном пути. Можно двигаться дальше.

4.Решите уравнение .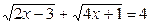

Решение

В данном уравнении переменная содержится под двум радикалами и уединить корни не удаётся. В таком случае для решения уравнения, как правило, приходится возводить в степень дважды.

Возведем обе части уравнения в квадрат: .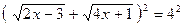

Получим 2х-3 + 2 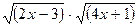+4х+1=16,

или 2х-3 + 2 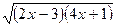+4х+1=16.

Данное уравнение содержит один радикал; оставим его в левой части, а все остальные члены уравнения из правой части перенесем с противоположным знаком в левую часть.

Получим: 2 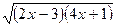=16-2х+3-4х-1 ð 2 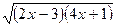=18- 6х /:2.

Получим: 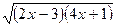=9 - 3х.

Снова возведем обе части уравнения в квадрат:

(2х – 3)(4х + 1) = 81 – 54х + 9х², х² – 44х + 84 = 0, откуда х₁ = 2, х₂ = 42.

⇐ Предыдущая 123 4 Следующая ⇒