Хелпикс

Главная

Контакты

Случайная статья



Вариант II. III уровень. Вариант I. Вариант II. VI. Подведение итогов.. Домашнее задание.

⇐ ПредыдущаяСтр 3 из 3


Вариант II

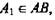
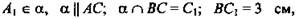
1. Дано: ABCD - параллелограмм; 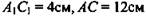(рис. 8).

Доказать: ΔADC ~ ΔА1ВС1.

Найти: AD.

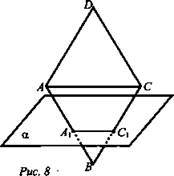
Решение:

1)

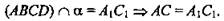
2) ΔАВС и ΔА1ВС1: ∠B - общий, ∠ACB = ∠A1C1B, ∠CAB = ∠C1A1B соответствующие при АС || А1С1, значит, ΔАВС ~ ΔА1ВС1.

3) 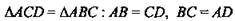(по свойству параллелограмма), АС — общая.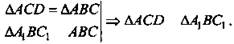

4) Из п. 2 следует, что ΔАВС ~ Δ А1ВС1. 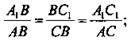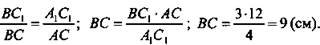(Ответ: 9 см.)

2. Дано: ABCD - параллелограмм; 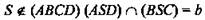(рис. 9).

Доказать: b || (ABCD).

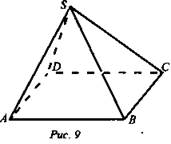
Доказательство: Пусть b ∩ (ABCD), значит в плоскости (SBC), b ∩ ВС, в плоскости (SAD); b ∩ AD, следовательно, 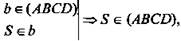но это противоречит условию, значит, b || (ABCD).

III уровень

Вариант I

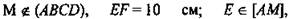
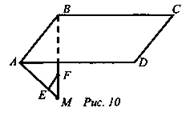
1. Дано: ABCD -параллелограмм; 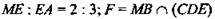(рис. 10).

Найти: АВ.

Решение:

1) 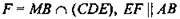по теореме о параллельности прямой и плоскости.

2) ΔABM ~ ΔFEM (по трем углам) 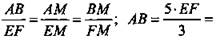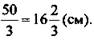(Ответ: )

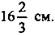2. Дано: 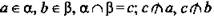(рис. 11.

Доказать: а || b.

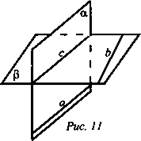
Доказательство:

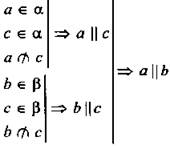по теореме о трех параллельных прямых.

 

Вариант II

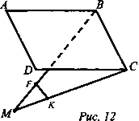
1. Дано:

 ABCD - ромб; 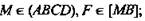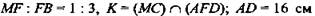(рис. 12).

Найти: FK.

Решение:

1) 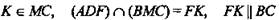по теореме о параллельности прямой и плоскости.

2) ABCD - ромб, значит, BC = AD. ΔMFK ~ ΔМВС (по трем углам.

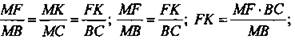
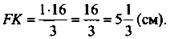(Ответ: )

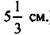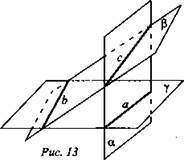
2. Дано: 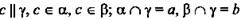(рис. 13).

Доказать: а || b.

 

Доказательство:

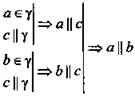по теореме о трех параллельных прямых.

 

VI. Подведение итогов.

Домашнее задание.

I уровень: № 32 (разобрана в учебнике), № 92.

II уровень: № 33, № 92.

 

Задача 33

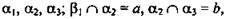
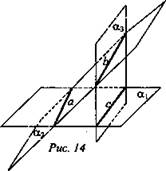
Дано: 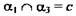(рис. 14).

Доказать: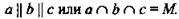

Доказательство:

1) Никакие две прямые не пересекаются, тогда они параллельны, так как, а и b ∈ α2, значит, а || b. Аналогично b || с, а || с.

2) Любые две прямые, например, а ∩ b = М, значит, М ∈ α1, М ∈ α2, M ∈ α3, а тогда, значит, М лежит во всех плоскостях и b ∩ с = М.

3) а = b, тогда прямые являются пересечением всех трех плоскостей α1, α, α3, а значит, плоскости проходят через одну прямую, что противоречит условию.




⇐ Предыдущая123
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.