
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Организационный этап урока. Актуализация опорных знаний
Стр 1 из 4Следующая ⇒
| 01.11.2021 Алгебра | ||
| Тема урока | Область определения и множество значений тригонометрических функций | |
| Класс | 11 класс | |
| Тип урока | Урок изучения нового учебного материала | |
| Номер урока по данной теме | Первый урок | |
| Цель урока | Введение понятий тригонометрических функций и формирование умения исследовать область определения и множество значений тригонометрических функций | |
| Деятельность учителя | Деятельность учащихся | |
| Ход урока | ||
Организационный этап урока
Здравствуйте, ребята! Будьте добры, подготовьте учебник, тетрадь, ручку, карандаш, линейку, циркуль.
Закройте правый столбец моего конспекта ( уменьшив рамку рабочего стола справа налево. Правый столбец – это подсказка ( если вы не справитесь с заданием)
Актуализация опорных знаний
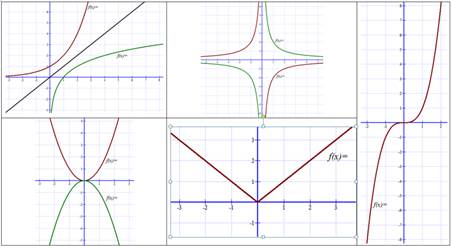
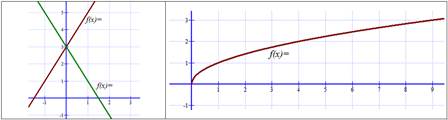
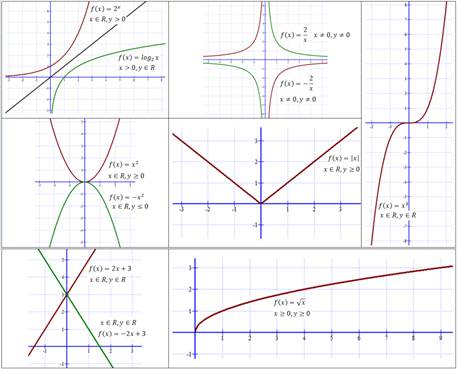 Пример ответа: формула
Пример ответа: формула 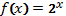 задаёт показательную функцию, область определения образуют положительные числа, множество значений – все действительные числа; формула
задаёт показательную функцию, область определения образуют положительные числа, множество значений – все действительные числа; формула  задает обратную пропорциональность, область определения данной функции – все действительные числа, кроме нуля, множество значений функции – также все действительные числа, кроме нуля.
задает обратную пропорциональность, область определения данной функции – все действительные числа, кроме нуля, множество значений функции – также все действительные числа, кроме нуля.
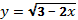 ; 2)
; 2) 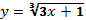 ; 3)
; 3) 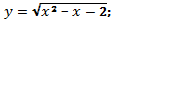 4)
4) 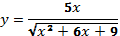 ; 5)
; 5) 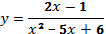 ; 6)
; 6) 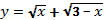 ;
7)
;
7) 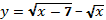 ; 8)
; 8) 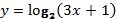 ; 9)
; 9) 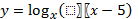 .
.
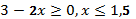 ; 5) Действие деления выполнимо, когда знаменатель не равен нулю, таким образом,
; 5) Действие деления выполнимо, когда знаменатель не равен нулю, таким образом, 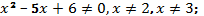 9) Логарифмом положительного числа b по основанию a, где
9) Логарифмом положительного числа b по основанию a, где 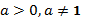 , называется показатель степени, в которую надо возвести a,чтобы получить b. Значит, имеем
, называется показатель степени, в которую надо возвести a,чтобы получить b. Значит, имеем 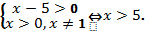
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|