
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
В треугольнике МNК стороны МN=12см, МК=10см, МD – биссектриса, КD=5см. Найдите DN.
2 часть
6а.Точка Р находится вне двух параллельных плоскостей. Две прямые, которые проходят через неё, пересекают ближнюю плоскость в точках А1 и А2, а ту, что находится дальше – в точках В1 и В2. Найдите В1В2, если А1А2 = 6,5м, РА1=А1В1.
6п.Точка Р находится вне двух параллельных плоскостей. Две прямые, которые проходят через неё, пересекают ближнюю плоскость в точках А1 и А2, а ту что находится дальше - в точках В1 и В2. Найдите длину отрезка В1В2, если А1А2=6см и РА1:А1В1=3:2.
6м.Плоскости α и β параллельны. Отрезок АВ расположен в плоскости α. Через его концы и точку К, которая находится между плоскостями, проведены прямые АК и ВК, которые пересекают плоскость β соответственно в точках А1 и В1. Найдите длину отрезка АА1, если А1В1 : АВ = 3 : 4; АК = 6 дм.
7а.Все ребра прямой треугольной призмы имеют длину 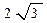 см. Найдите объем призмы.
см. Найдите объем призмы.
7п.В наклонной треугольной призме стороны основания равны 4, 13 и 15 см. Боковое ребро 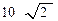 см образует с плоскостью основания угол 45о. Найдите объем призмы.
см образует с плоскостью основания угол 45о. Найдите объем призмы.
7м.В основании прямой призмы лежит равнобедренный треугольник с углом β при основании и радиусом вписанной окружности r. Диагональ боковой грани, которая содержит основание этого треугольника, образует угол α с плоскостью основания призмы. Найдите объем призмы.
3 часть
8а.Через вершину конуса проведена плоскость под углом 450 к плоскости основания. Эта плоскость пересекает основание по хорде, расстояние до которой от вершины 6 см. Найдите объем конуса, если длина радиуса – 5 см.
8п.В усеченном конусе, отношение площадей оснований равно 4, образующая длиной 4 см наклонена к плоскости основания под углом 300. Найдите объем конуса.
8м. В усеченном конусе высота, образующая и боковая поверхность равны соответственно Н, L и S. Найдите площадь осевого сечения.
10 вариант
1 часть
1. Определите вид треугольника со сторонами 3см, 5см и 7см.
А) прямоугольный; Б) остроугольный; В) тупоугольный; Г) определить нельзя.
2. Периметр ромба равен 80 см, а один из его углов 60°. Найдите длину меньшей диагонали.
А) 20 см; Б) 30 см; В) 10 см; Г) 40 см.
3. Найдите скалярное произведение векторов 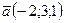 и
и 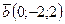 .
.
А)4; Б) 2; В) -4; Г) -6.
4. Основанием прямой призмы является равнобедренный треугольник с основанием 10 см и боковой стороной 6 см. Высота призмы равна 5 см. Найдите площадь боковой поверхности призмы.
А) 330 см2; Б) 1800 см2 В) 110 см2 Г) 55 см2.
5. Прямоугольник со сторонами 10 см и 4 см, вращается около большей стороны. Найдите площадь поверхности тела вращения.
А) 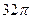 см2; Б)
см2; Б) 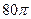 см2; В)
см2; В) 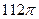 см2; Г)
см2; Г)  см2.
см2.
2 часть
6а.Есть две параллельные плоскости и точка К, которая не находится между ними. Две прямые, которые проходят через точку К, пересекают ближнюю плоскость в точках С1 и С2, а другую - в точках D1 и D2 соответственно. Найдите С1С2, если D1D2 = 17 м, КС1 = С1D1.
6п.Есть две параллельные плоскости и точка К, которая не находится между ними. Две прямые, которые проходят через точку К, пересекают ближнюю плоскость в точках С1 и С2, а другую - в точках D1 и D2 соответственно. Найдите длину отрезка D1D2, если С1С2 = 10 см, КС1 : С1D1 = 2 : 3.
6м.Плоскости α и β параллельны. Отрезок АВ расположенный в плоскости α. Через его концы и точку К, которая находятся между плоскостями, проведены прямые АК и ВК. АК пересекает плоскость β в точке А1, а ВК – в точке В1. Найдите длину ВВ1,если АВ : А1В1 = 2 : 3, ВК =12 м.
7а.Объем прямой призмы, основание которой – правильный треугольник, равен 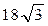 см3,, а её высота 8 см. Найдите сторону основания призмы.
см3,, а её высота 8 см. Найдите сторону основания призмы.
7п.В основании наклонной призмы лежит параллелограмм со сторонами 6 дм и 12 дм и острым углом 60о. Боковое ребро призмы равно 14 дм и образует с плоскостью основания угол 30о. Найдите объем призмы.
7м.В основании прямой призмы лежит равнобедренный треугольник с углом α при вершине и радиусом описанной окружности R. Диагональ боковой грани, которая содержит боковую сторону этого треугольника, образует с плоскостью основания угол β. Найдите объем призмы.
3 часть
8а.Через две образующие конуса проведена плоскость, которая пересекает основание по хорде, длиной 8 см. Эта плоскость образует с основанием угол 600. Найдите объем конуса, если радиус основания равен 5 см.
8п.Диагональ осевого сечения усеченного конуса делится осью на отрезки 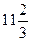 см и
см и 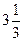 см. Зная, что образующая равна 13 см, определите его объем.
см. Зная, что образующая равна 13 см, определите его объем.
8м. В усеченном конусе определите площадь осевого сечения, если площади оснований равны Q и q, а площадь боковой поверхности — S.
11 вариант
1 часть
1. Найдите площадь кругового сегмента, если радиус круга 4дм, а соответствующий центральный угол равен 90°.
А) 4πдм²; Б) 4(π-2) дм²; В) 8(π-2) дм²; Г) 4(2-π) дм².
2. В равностороннем треугольнике высота равна 12дм. Найдите радиус вписанной в этот треугольник окружности.
А)4дм; Б)6дм; В)8дм; Г)2дм.
3. Среди точек 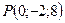 ,
, 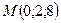 ,
, 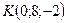 ,
, 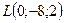 укажите пару точек, которые являются симметричными относительно оси
укажите пару точек, которые являются симметричными относительно оси 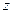 .
.
А) P и M; Б) M и L; В) P и K; Г) K и L.
4. Сторона основания правильной четырехугольной пирамиды 5 см, а апофема 12 см. Найдите площадь боковой поверхности пирамиды.
А)180см2; Б)240см2; В)120см2; Г)90см2.
5. Высота конуса 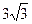 см, осевое сечение – правильный треугольник. Найдите площадь боковой поверхности конуса.
см, осевое сечение – правильный треугольник. Найдите площадь боковой поверхности конуса.
А) 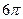 см2; Б)
см2; Б) 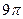 см2; В)
см2; В) 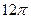 см2; Г)
см2; Г) 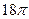 см2.
см2.
2 часть
6а.Расстояние от точки М до всех сторон квадрата равно 13 см. Найдите расстояние от точки М до плоскости квадрата, если сторона квадрата равна 10 см.
6п.Из точки, удаленной от плоскости на 4 см, проведены две наклонные к этой плоскости длиной 5 см и 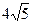 см. Угол между проекциями этих наклонных 600. Найдите расстояние между основаниями наклонных.
см. Угол между проекциями этих наклонных 600. Найдите расстояние между основаниями наклонных.
6м.Из точки к плоскости проведены две наклонные, длины которых 25 см и 30 см. Разность проекций этих наклонных на плоскость равна 11 см. Найдите расстояние от данной точки до плоскости.
7а.Плоский угол при вершине правильной треугольной пирамиды равен 600, а боковое ребро 6см. Найдите площадь боковой поверхности пирамиды.
7п.Боковое ребро правильной треугольной пирамиды равен 12 см и образует с плоскостью основания угол 300. Найдите площадь боковой поверхности пирамиды.
7м.В основании пирамиды лежит равнобедренный треугольник с основанием а и углом α при вершине. Все боковые грани пирамиды образуют с плоскостью основания угол φ. Найдите площадь боковой поверхности пирамиды.
3 часть
8а.Один цилиндр имеет высоту 2,4м и диаметр основания 1м; другой цилиндр имеет высоту 1,2м и диаметр основания 0,5м. Сравните объемы обоих цилиндров.
8п.Найдите наибольший объем цилиндра, площадь полной поверхности которого равен 54 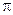 см2, если длина радиуса основания R принадлежит отрезку
см2, если длина радиуса основания R принадлежит отрезку 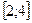 .
.
8м. В правильной треугольной призме через сторону нижнего основания и противолежащую вершину верхнего основания проведено сечение. Из вершины, что не принадлежит этой стороне, к плоскости сечения проведен перпендикуляр, который равен а и образует с плоскостью нижнего основания угол φ. Найдите объем цилиндра, вписанного в данную призму.
12 вариант
1 часть
1. Найдите площадь кругового сегмента, если радиус круга 12м, а соответствующий центральный угол равен 30°.
А) 6(3-π) м²; Б) 6(π-3) м²; В)12(3-π) м²; Г) 12(π-3) м².
2. В равностороннем треугольнике высота равна 12дм. Найдите радиус описанной около этого треугольника окружности.
А)4дм; Б)6дм; В)8дм; Г)2дм.
3. Среди точек 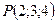 ,
,  ,
, 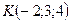 ,
,  укажите пару точек, которые являются симметричными относительно плоскости
укажите пару точек, которые являются симметричными относительно плоскости 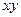 .
.
А) P и M; Б) M и L; В) P и L; Г) K и L/
4. Боковая грань правильной четырехугольной пирамиды - правильный треугольник, периметр которого 36 см. Найдите площадь боковой поверхности пирамиды.
А) 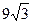 см2; Б)
см2; Б) 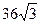 см2; В)
см2; В) 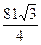 см2; Г)
см2; Г) 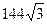 см2.
см2.
5. Осевое сечении конуса – правильный треугольник с площадью 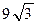 см2. Найдите площадь поверхности конуса.
см2. Найдите площадь поверхности конуса.
А) 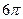 см2; Б)
см2; Б) 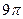 см2; В)
см2; В) 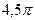 см2; Г)
см2; Г) 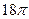 см2.
см2.
2 часть
6а.Расстояние от точки М до всех вершин квадрата равно 5 см. Найдите расстояние от точки М до плоскости квадрата, если диагональ квадрата равна 6 см.
6п.Из точки, удаленной от плоскости на 12 см, проведены две наклонные к этой плоскости длиною 13 см и 20 см. Расстояние между основаниями наклонных равно 19 см. Найдите угол между проекциями этих наклонных.
6м.Из точки к плоскости проведены две наклонные. Разность между длинами наклонных равна 5 см. Проекции этих наклонных на плоскость соответственно равны 18 см и 7 см. Найдите расстояние от данной точки до плоскости.
7а.Плоский угол при вершине правильной треугольной пирамиде равен 450, а боковое ребро 8см. Найдите площадь боковой поверхности пирамиды.
7п.Боковая грань правильной треугольной пирамиды наклонена к плоскости основания под углом 600. Найдите площадь боковой поверхности, если высота пирамиды равна 6 см.
7м.В основании пирамиды лежит равнобедренный треугольник с боковой стороной b и углом α при вершине. Все боковые грани наклонены к плоскости основания под углом φ. Найдите площадь боковой поверхности пирамиды.
3 часть
8а.Два цилиндра имеют одинаковые основания. Объем первого цилиндра равен 7,5 дм3, а его высота – 21см. Высота второго цилиндра равна7см. Чему равен объем второго цилиндра?
8п.Найдите наименьшую возможную площадь полной поверхности цилиндра, если известно, что его объем равен 16 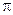 см3, а длина радиуса основания R принадлежит отрезку
см3, а длина радиуса основания R принадлежит отрезку 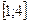 .
.
8м. В основании прямой призмы лежит прямоугольный треугольник с острым углом α. Через диагонали двух боковых граней, которые содержат стороны угла α, проведено сечение, площадь которого S. Угол между этими диагоналями равен β. Найдите объем цилиндра, описанного около данной призмы.
13 вариант
1 часть
1. Стороны параллелограмма равны 6дм и 10дм, а одна из его диагоналей 13дм. Найдите другую диагональ параллелограмма.
А) 6 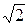 дм; Б) 6
дм; Б) 6 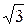 дм; В)
дм; В) 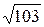 дм; Г) 9,5дм.
дм; Г) 9,5дм.
2. Проекция катета на гипотенузу, длина которой 16см, равна 4см. Найдите данный катет.
А) 9см; Б) 8см; В) 10см; Г) 6см.
3. Какой из предложенных векторов коллинеарен вектору 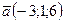 ?
?
А) ; Б) ; В) ; Г) .
4. Основание прямой призмы - прямоугольник со сторонами 8см и 6см. Боковое ребро 10см. Найдите площадь полной поверхности призмы.
А) 376см2; Б) 62см2; В) 124см2; Г) 328 см2.
5. Площадь осевого сечения конуса 8 см2, а его высота 4 см. Найдите объем конуса.
А) 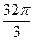 см3; Б)
см3; Б) 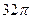 см3; В)
см3; В) 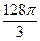 см3; Г)
см3; Г) 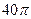 см3.
см3.
2 часть
6а.При параллельном переносе точка А(-3;1;2) переходит в точку А′(5;-1;4). Найдите формулы этого параллельного переноса.
6п.Дано точки А(-7;3;-2) и В(4;-5;1). Найдите формулы параллельного переноса, при котором точка А переходит у точку В, и переноса, при котором В переходит в А.
6м.Существует ли параллельный перенос, при котором точка К(-3;-2;5) переходит в точку К′ (2;4;1), а точка F(2;-7;4) – в точку F′(7;-1;8)?
7а.В правильной треугольной призме радиус окружности, вписанной в основание, равен 2 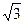 см. Диагональ боковой грани образует с плоскостью основания угол 45о. Найдите площадь боковой поверхности призмы.
см. Диагональ боковой грани образует с плоскостью основания угол 45о. Найдите площадь боковой поверхности призмы.
7п.Диагональ боковой грани правильной треугольной призмы равна d и образует с плоскостью основания угол α. Найдите площадь боковой поверхности призмы.
7м.Основой наклонной призмы АВСА1В1С1 является правильный треугольник АВС со стороной а. Вершина А1 проектируется в центр нижнего основания, а ребро АА1 образует с плоскостью основания угол 60о. Найдите площадь боковой поверхности призмы.
3 часть
8а.Развертка боковой поверхности цилиндра - прямоугольник, одна из сторон которого вдвое больше другой. Боковая поверхность цилиндра равна 20 дм2. Найдите его полную поверхность, если образующая цилиндра - меньшая сторона его развертки.
8п.Зная, что полная поверхность цилиндра равна105π см2, а боковая поверхность равна 80π см2, найдите объем цилиндра.
8м. В равностороннем цилиндре, радиус основания которого равен R, через точку окружности верхнего основания и точку окружности нижнего основания проведена прямая, которая наклонена к плоскости основания под углом α. Найдите расстояние от этой прямой до оси цилиндра.
14 вариант
1 часть
1. Стороны параллелограмма равны 7см и 9см, а одна из его диагоналей
равна 8см. Найдите вторую диагональ параллелограмма.
А) 14см; Б) 12 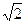 см; В) 10
см; В) 10 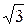 см; Г) 10,5см.
см; Г) 10,5см.
2. Катет прямоугольного треугольника равен 8см, а его проекция на гипотенузу – 4см. Найдите гипотенузу.
А) 14см; Б) 12см; В) 10см; Г) 16см.
3. Какой из предложенных векторов коллинеарен вектору 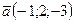 ?
?
А) ; Б) ; В) ; Г) .
4. Основание прямой призмы - прямоугольный треугольник с катетами 6 см и 8 см. Найдите площадь полной поверхности призмы, если высота призмы – 5см.
А) 180см2; Б) 72см2; В) 144см2; Г) 168см2.
5. Площадь осевого сечения конуса 16 см2, а диаметр основания 4 см. Найдите объем конуса.
А) 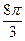 см3; Б)
см3; Б) 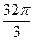 см3; В)
см3; В) 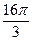 см3; Г)
см3; Г) 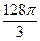 см2.
см2.
2 часть
6а.При параллельном переносе точка М(-4;-6;8) переходит у точку М′(-10;2;-4). Найдите формулы этого параллельного переноса.
6п.Дано точки М(-4;3;1) и К(8;-5;2). Найдите формулы параллельного переноса, при котором точка М, переходит у точку К, и переноса, при котором точка К, переходить у точку М.
6м.Существует ли параллельный перенос, при котором точка А(-7;-8;3) переходит в точку А′ (10;-2;-5), а точка М(0;4;-8) – у точку М′(2;-10;12)?
7а.В правильной треугольной призме диагональ боковой грани равна 13см. Найдите площадь боковой поверхности призмы, если радиус окружности, вписанной в основание, равен 2 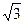 см.
см.
7п.Диагональ боковой грани правильной треугольной призмы образует с боковым ребром угол β. Радиус окружности, описанной около боковой грани, равен R. Найдите площадь боковой поверхности призмы.
7м.Все ребра прямой треугольной призмы имеют одинаковую длину. Площадь полной поверхности призмы равна 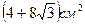 . Найдите площадь основания призмы.
. Найдите площадь основания призмы.
3 часть
8а.Найдите площадь боковой поверхности цилиндра, высота которого равна 5см, если известно, что при увеличении его высоты на 4см, объем увеличивается на 36π см3.
8п.Найдите диагональ осевого сечения цилиндра, зная, что объем цилиндра равен240π см3, а боковая поверхность 120π см2.
8м. Радиус основания равностороннего цилиндра равен R. Через точку окружности верхнего основания и точку окружности нижнего основания проведена прямая. Расстояние от этой прямой до оси цилиндра равно b. Найдите угол наклона этой прямой к плоскости основания цилиндра.
15 вариант
1 часть
1. Внутренний угол правильного многоугольника при одной из его вершин равен 150°. Сколько сторон имеет этот многоугольник?
А) 9; Б)10; В) 11; Г) 12.
2. В трапеции ABCD BC – меньшее основание. На основании AD взята точка К так, что ВК ||CD. 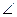 ABK=80°,
ABK=80°, 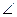 BKA=40°. Найдите угол АВС.
BKA=40°. Найдите угол АВС.
А) 130°; Б) 120°; В) 140°; Г) 60°.
3. Найдите координаты середины отрезка АВ, если А(-2;3;4), В(2;3;8).
А) (0;3;6); Б) (-4;0;-4); В) (-2;0;-2); Г) (0;6;12).
4. Объем треугольной пирамиды равен 24 дм3. Высота пирамиды 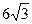 дм. Найдите площадь основания данной пирамиды.
дм. Найдите площадь основания данной пирамиды.
А) 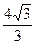 дм2; Б)
дм2; Б) 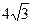 дм2; В)
дм2; В) 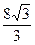 дм2; Г) 4дм2.
дм2; Г) 4дм2.
5. Осевое сечение цилиндра – квадрат, диагональ которого равна 4 см. Найдите объем цилиндра.
А)  см3; Б)
см3; Б) 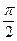 см3; В)
см3; В) 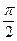 см3; Г)
см3; Г) 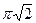 см3.
см3.
2 часть
6а.При каком значении 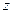 векторы
векторы 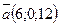 и
и 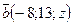 являются перпендикулярными?
являются перпендикулярными?
6п.Векторы 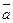 и
и 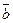 перпендикулярны, и
перпендикулярны, и 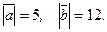 Найдите
Найдите 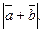
6м.Дано: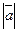 =13;
=13; 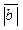 =19;
=19; 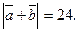 Найдите
Найдите 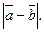
7а.Основа пирамиды – прямоугольный треугольник с катетами 6см и 8см. Высота пирамиды равна 10см. Найдите объем пирамиды.
7п.В основании пирамиды лежит прямоугольный треугольник с катетом а и прилежащим острым углом β. Найдите объем пирамиды, если все боковые ребра пирамиды наклонены к ее основанию под углом α.
7м.В правильной треугольной пирамиде двугранный угол при основании равен α. Отрезок, который соединяет середину высоты пирамиды с серединой апофемы, равен а. Найдите объем пирамиды.
3 часть
8а.Стороны Δ АВС касаются сферы радиуса 5 см. Найдите расстояние от центра сферы до плоскости треугольника, если его стороны равны 10 см, 10 см, 12 см.
8п.Высота правильной четырехугольной призмы 2 см, сторона основания 4 см. Найдите радиус описанной около пирамиды сферы.
8м. Найдите объем правильной треугольной призмы, если радиус описанной около неё сферы равен R. Этот радиус, проведенный к вершине призмы, образует угол φ с боковой гранью, которая содержит эту вершину.
16 вариант
1 часть
1. Внутренний угол правильного многоугольника при одной из его вершин равен 144°. Сколько сторон имеет этот многоугольник?
А) 9; Б) 10; В) 11; Г) 12.
2. В равнобокой трапеции диагональ перпендикулярна её боковой стороне и образует с большим основанием угол 25°. Найдите тупой угол трапеции.
А) 115°; Б) 155°; В) 130°; Г) 105°.
3. Найдите координаты середины отрезка АВ, если А(-2;4;-8), В(6;8;2).
А) (4;12;-6); Б) (-2;-6;6); В) (2;6;-6); Г) (-12;32;-16).
4. Основа пирамиды – прямоугольный треугольник с катетами 6см и 8см. Высота пирамиды 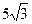 см. Найдите объем пирамиды.
см. Найдите объем пирамиды.
А) 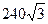 дм3; Б)
дм3; Б) 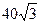 дм3; В)
дм3; В) 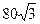 дм3; Г) 40дм3.
дм3; Г) 40дм3.
5. Осевое сечение цилиндра – квадрат, периметр которого равен 16см. Найдите объем цилиндра.
А)  см3; Б)
см3; Б) 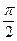 см3; В)
см3; В) 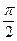 см3; Г)
см3; Г) 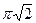 см3.
см3.
2 часть
6а.При каком значении х векторы 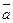 (6; 0; 12) и
(6; 0; 12) и 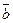 (х; 13; 4) перпендикулярны?
(х; 13; 4) перпендикулярны?
6п.Векторы 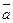 и
и 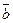 перпендикулярны, и
перпендикулярны, и 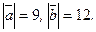 Найдите
Найдите 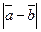 .
.
6м.Дано: 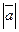 =11;
=11; 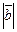 =23;
=23; 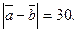 Найдите
Найдите 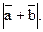
7а.Высота правильной треугольной пирамиды равна 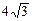 см, а сторона её основания –
см, а сторона её основания – 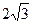 см. Найдите объем пирамиды.
см. Найдите объем пирамиды.
7п.В основании пирамиды лежит равнобедренный треугольник с углом α при основании и боковой стороной b. Найдите объем пирамиды, если все ее боковые ребра наклонены к её основанию под углом β.
7м.В правильной треугольной пирамиде боковое ребро образует с высотой угол α. Найдите объем пирамиды, если расстояние от середины высоты до бокового ребра равно а.
3 часть
8а.Все стороны Δ АВС касаются сферы радиуса 5 см. Найдите расстояние от центра сферы до плоскости треугольника, если АВ = 13см, ВС = 14см, СА = 15см.
8п.Радиус шара 9см. В неё вписана правильная четырехугольная призма, высота которой 14 дм. Найдите сторону основания призмы.
8м. Найдите объем правильной четырехугольной призмы, если радиус описанной около неё сферы равен R. Этот радиус, проведенный к вершине призмы, образует угол φ с боковой гранью, которая содержит эту вершину.
17 вариант
1 часть
1. Угол при основании равнобедренного треугольника равен 75º, а основание - 6см.
Найдите длину радиуса описанной окружности.
А) 9 см; Б) 6см; В)12см; Г) 6 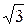 см.
см.
2. Как изменится площадь квадрата, если каждую его сторону увеличить в 9 раз?
А)увеличится в 9 раз; Б)увеличится в у 12 раз;
В)увеличится в у 6 раз; Г) другой ответ.
3. Найдите координаты вектора 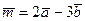 , если
, если 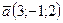 и
и 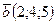 .
.
А) (0;14;-11); Б) (0;-14;11); В) (0;-14;-11); Г) (0;14;11).
4. Объем четырехугольной призмы 72 дм3, а площадь основания призмы 12 см2. Найдите высоту этой призмы.
А) 24 см; Б) 6см; В)12см; Г) 6 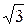 см.
см.
5. Объем шара 36 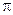 см3. Найдите диаметр шара.
см3. Найдите диаметр шара.
А) 6см; Б) 3см; В) 1,5см; Г) 12см.
2 часть
6а.Через концы отрезка АВ и его середину М проведены параллельные прямые, которые пересекают некоторую плоскость в точках А1, В1, М1. Найдите длину отрезка ММ1, если отрезок АВ не пересекает плоскость и АА1=5м, ВВ1=7м.
6п.Через конец А отрезка АВ проведена плоскость. Через конец В и точку С этого отрезка проведены параллельные прямые, которые пересекают плоскость в точках В1 и С1. Найдите длину отрезка ВВ1, если СС1=15 см, АС:ВС=2:3.
6м.Прямая а параллельна плоскости α. Через точки А и В прямой а проведены параллельные прямые, которые пересекают плоскость α в точках А1 и В1 соответственно. Найдите площадь четырехугольника АА1В1В, если А1В1=29см, АА1 = 25 см, А1В = 36 см.
7а.Правильный треугольник со стороной 6 см вращается около стороны. Найдите площадь поверхности тела вращения.
7п.Равнобедренный треугольник с боковой стороной 13 см и основанием 10 см вращается около основания. Найдите площадь поверхности тела вращения.
7м.Равнобедренный треугольник, основание которого а и острый угол при вершине α, вращается около оси, которая лежит в плоскости треугольника, проходит через его вершину и перпендикулярна боковой стороне. Найдите площадь поверхности тела вращения.
3 часть
8а.Полная поверхность прямоугольного параллелепипеда, основанием которого служит квадрат, равна 264 см2. Найдите сторону основания параллелепипеда, если его высота равна 8 см.
8п.Основанием призмы является квадрат со стороной: 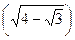 см. Одна из боковых граней тоже квадрат, а другая - ромб с углом 60о. Найдите полную поверхность призмы.
см. Одна из боковых граней тоже квадрат, а другая - ромб с углом 60о. Найдите полную поверхность призмы.
8м. Основание правильной призмы - шестиугольник со стороной 3 дм, высота призмы равна 13дм. Найдите площадь сечения, проведенного через две противоположные стороны верхнего и нижнего оснований призмы.
18 вариант
1 часть
1. В треугольнике одна сторона равна 8 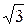 см, а противолежащий угол равен 60º. Найдите длину радиуса описанной окружности.
см, а противолежащий угол равен 60º. Найдите длину радиуса описанной окружности.
А) 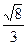 см; Б) 4
см; Б) 4 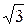 см; В) 6см; Г) 8см.
см; В) 6см; Г) 8см.
2. Во сколько раз надо уменьшить стороны квадрата, чтобы его площадь уменьшилась в 25 раз?
А)5; Б)10; В)25; Г)50.
3. Найдите координаты вектора 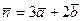 , если
, если 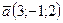 и
и 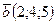 .
.
А) (13;-5;16); Б) (-13;5;16); В) (13;5;-16); Г) (13;5;16).
4. В основании прямой четырехугольной призмы – ромб, площадь которого 12см2. Высота призмы 10 см. Найдите объем призмы.
А) 120 см3; Б) 40см3; В)60см3; Г) 1440см3.
5. Диаметр шара равен 12 см. Найдите объем шара.
А) 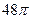 см3; Б)
см3; Б) 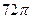 см3; В)
см3; В)  см3; Г)
см3; Г) 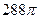 см3.
см3.
2 часть
6а.Через концы отрезка АВ и его середину – точку М – проведены параллельные прямые, которые пересекают некоторую плоскость в точках А1, В1 и М1. Найдите длину отрезка ММ1, если отрезок. АВ не пересекает плоскость и АА1=36 см, ВВ1=48см.
6п.Через конец А отрезка АВ проведена плоскость. Через конец В и точку С этого отрезка проведены параллельные прямые, которые пересекают плоскость в точках В1 и С1 соответственно. Найдите длину отрезка ВВ1, если СС1 = 8,1 см, АВ : АС = 11:9.
6м.Прямая а параллельна плоскости α. Через точки А и В прямой а проведены параллельные прямые, которая пересекает плоскость α в точках А1 и В1 соответственно. Найдите площадь четырехугольника АА1В1В, если А1В1=25 см, АВ1=29 см, ВВ1=5см.
7а.Правильный треугольник со стороной 10см вращается около стороны. Найдите площадь поверхности тела вращения.
7п.Равнобедренный треугольник с боковой стороной 10см и основой 12см вращается около основания. Найдите площадь поверхности тела вращения.
7м.Равнобедренный треугольник, боковая сторона которого b и угол при основании β, вращается около оси, которая лежит в плоскости треугольника, проходит через вершину угла при основании и перпендикулярна боковой стороне. Найдите площадь поверхности тела вращения.
3 часть
8а.В прямоугольном параллелепипеде его измерения относятся как 1:2:3. Полная поверхность параллелепипеда равна 352 см2. Найдите его измерения.
8п.Основа наклонного параллелепипеда - квадрат со стороной а, одна из вершин другого основания проектируется в центр этого квадрата. Высота параллелепипеда равна Н. Найдите площадь боковой поверхности параллелепипеда.
8м. Правильная шестиугольная призма, боковые грани которой – квадраты, пересекается плоскостью, которая проходит через сторону нижнего основания и противолежащую ей сторону верхнего основания. Сторона основания 5 дм. Найдите площадь образованного сечения.
19 вариант
1 часть
1. В треугольнике МNК стороны МN=12см, МК=10см, МD – биссектриса, КD=5см. Найдите DN.
А) 6см; Б) 7см; В) 24см; Г) 17см.
2. В ΔАВС стороны АВ= 4см, АС= 4 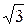 см,
см, 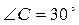 . Найдите
. Найдите 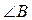 .
.
А) 90°; Б) 60° или 120°; В) 45°; Г) решений нет.
3. Точки 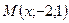 и
и 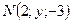 симметричны относительно точки
симметричны относительно точки 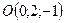 . Найдите
. Найдите 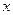 и
и 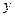 .
.
А) 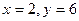 ; Б)
; Б) 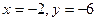 ; В)
; В)  ; Г)
; Г) 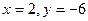 .
.
4. Высота правильной четырехугольной пирамиды 3 см, а апофема 5 см. Найдите площадь боковой поверхности пирамиды.
А) 80см2; Б) 40см2; В) 20см2; Г) 160см2.
5. Осевое сечение конуса – равносторонний треугольник со стороной 6 см. Найдите площадь поверхности конуса.
А) 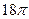 см2; Б)
см2; Б) 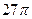 см2; В)
см2; В) 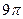 см2; Г)
см2; Г) 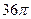 см2.
см2.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|