Задача 2.. Задача 3.

Задача 2.

Стороны AB и BC параллелограмма ABCD пересекают плоскость 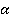. Докажите, что прямые AD и DC также пересекают плоскость .

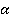Дано: ABCD – параллелограмм,

Доказать: прямые AD и DC пересекают плоскость .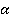

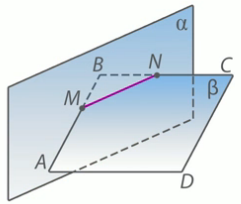
Рис. 13.

Доказательство: (Рис. 13.)

Обозначим плоскость АВС как 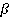. Тогда плоскост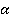и и 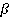пересекаются по прямой MN. Прямая АВ пересекается с плоскостью 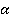, и прямые АВ и CD параллельны (как стороны параллелограмма). Тогда, согласно лемме, прямая CD также пересекается с плоскостью 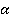. Аналогично, прямая ВC пересекается с плоскостью 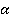, и прямые ВС и АD параллельны (как стороны параллелограмма). Тогда, согласно лемме, прямая АD также пересекается с плоскостью 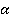, что и требовалось доказать.

Давайте найдем эти точки пересечения. Пусть прямая CD пересекается с плоскостью 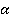в точке Q, а прямая АD пересекается с плоскостью 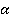в точке F.

Плоскост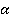и и 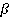пересекаются по прямой MN, значит все их общие точки лежат на этой прямой. Продолжим прямые CD и АD до их пересечения с прямой MN и получим соответственно точки Q и F (Рис. 14.).

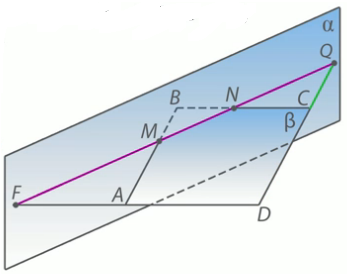
Рис. 14.

Задача 3

Задача 3.

Средняя линия трапеции лежит в плоскости 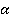, не совпадающей с плоскостью 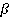. Пересекаются ли прямые, содержащие основания трапеции, с плоскостью ?

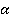Дано: ABCD – трапеция, MN – средняя линия.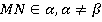

Найти: пересекаются ли прямые AD и ВC плоскость .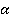

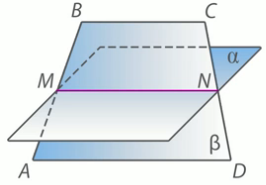
Рис. 15.

Решение: (Рис. 15.)

Вспомним, что средняя линия трапеции параллельна ее основанием. Значит, прямые AD и MN параллельны, а прямая MN принадлежит плоскости 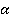. Значит, по признаку параллельности прямой и плоскости, AD параллельна плоскости .

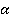Аналогично, прямые ВC и MN параллельны, а прямая MN принадлежит плоскости 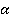. Значит, по признаку параллельности прямой и плоскости, ВC параллельна плоскости .

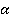Ответ задачи: нет, не пересекаются.

Задача 4

⇐ Предыдущая 123 Следующая ⇒