М1И ч.1 стр. 84

М1И ч.1 стр. 84

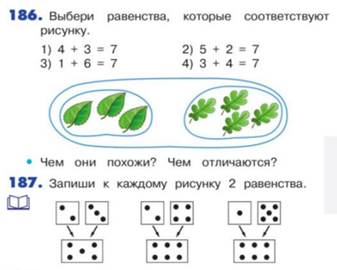
10. Раскройте методику изучения вычислительного приема для случаев +5, 6, 7, 8, 9. Составьте фрагмент урока ознакомления с приемом перестановки слагаемых (М1М, ч.2, стр. 15).

Методика изучения вычислительного приема для случаев: +5, 6, 7, 8, 9.

Если при вычислениях применить перестановку слагаемых, то все эти случаи сведутся к ранее изученным видам а + 1, а + 2, а + 3, а + 4. Для этого знакомятся с переместительным свойством сложения.

Раскрыть прием перестановки слагаемых, т. е. показать, когда именно в вычислениях используют переместительное свойство можно при решении практической задачи. Например, надо сложить вместе 2 мешка и 7 мешков муки, стоящие порознь. Как удобнее это сделать: принести 2 мешка к 7 или 7 мешков к двум? На основе таких упражнений дети приходят к выводу: легче к большему числу прибавить меньшее, а переставлять числа всегда можно – сумма от этого не изменится.

Затем показывают, как использовать прием перестановки слагаемых при решении примеров и задач на сложение в пределах 10. После этого составляется таблица сложения в пределах 10. Дети сами могут пояснить, почему включены только эти случаи и почему не включены остальные.

Первый способ: к 2 прибавить 2 – получится 4, затем 3 – получится 7.

Второй способ: к 5 прибавить 2 – получится 7.

Сколько всего книг на первом рисунке? (7)

А на втором? (7)

Давайте сравним оба равенства:

Чем отличаются слагаемые? (они одинаковые)

Отличается ли сумма слагаемых? (нет, сумма в двух примерах одинаковая)

Вывод: отличие в том, что слагаемые поменялись местами.

Изменился ли от этого результат сложения? Нет. Следовательно, от перестановки слагаемых результат сложения не изменяется.

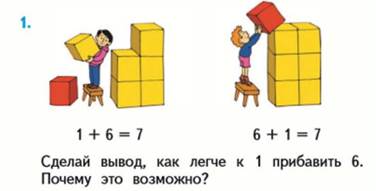
Ответ: легче прибавить 1 к 6. Это возможно потому, что от перестановки слагаемых сумма не меняется.

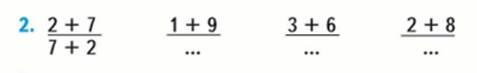
От перестановки слагаемых сумма не меняется, поэтому в данном задании мы просто поменяем числа местами – 9+1, 6+3, 8+2.

⇐ Предыдущая 1 23