
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Лемма Гейне-Бореля.
Лемма Гейне-Бореля.
Будем говорить, что семейство интервалов 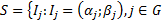 .
.
Служит покрытием отрезка [a; b] или покрывает отрезок [a; b] если 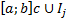 .
.
Следующие утверждения также выражает собой свойство полноты вещественных чисел и называется: лемма Гейне-Бореля.
Лемма 8.1
И всякого покрытия S отрезка [a, b] интервалами, можно выбрать конечное количество интервалов, покрывающее [a, b].
Доказательство:
Заметим, что любой отрезок [a, b’] 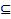 [a, b] покрывается семейством интервалов S. В - некоторые множества правых концов всех отрезков вида [a, b], где b’
[a, b] покрывается семейством интервалов S. В - некоторые множества правых концов всех отрезков вида [a, b], где b’ 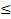 b. Где из покрытия S можно выбрать конечное подпокрытие (конечное число интервалов).
b. Где из покрытия S можно выбрать конечное подпокрытие (конечное число интервалов).
Очевидно, что B - не пустое множество 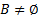 , поскольку левый конец a отрезка [a, b] покрывается некоторого интервалом I из семейства S. И внутри интервала всегда можно найти отрезок [a, b’]
, поскольку левый конец a отрезка [a, b] покрывается некоторого интервалом I из семейства S. И внутри интервала всегда можно найти отрезок [a, b’]
Пусть 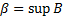 . Очевидно, что
. Очевидно, что 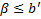 .
.
Докажем, что в этом неравенстве на самом деле равенство:
Предположим обратное: 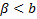
Из семейства S можно выбрать интервал, покрывающий точку 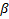 и число
и число 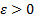 такое, что:
такое, что:
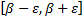 целиком располагался бы в интервале I (
целиком располагался бы в интервале I ( 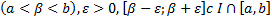 отрезок
отрезок 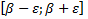 содержится в интервале I и отрезке [a, b])
содержится в интервале I и отрезке [a, b])
По свойству верхней грани (Sup B) множества B, существует такой элемент, который удовлетворяет неравенству: 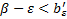 .
.
Отрезок [a, 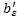 ] покрывается конечным числом интервалов, так как
] покрывается конечным числом интервалов, так как 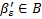 .
.
В этот же момент отрезок 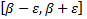 покрывается интервалом I. Поэтому отрезок
покрывается интервалом I. Поэтому отрезок 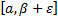 покрывается конечным числом интервалов из семейства S (
покрывается конечным числом интервалов из семейства S ( 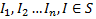 ). Это значит, что
). Это значит, что 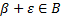 , что противоречит условию
, что противоречит условию 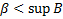 .
.
Полученное противоречие доказывает, что 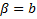 . Теперь уже нетрудно показать, что
. Теперь уже нетрудно показать, что 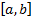 покрывается конечной системой интервалов из семейства S.
покрывается конечной системой интервалов из семейства S.
Действительно: 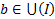
Выберем такой 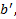 что отрезок [b’, b] целиком лежит в интервале I,
что отрезок [b’, b] целиком лежит в интервале I, 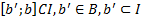 .
. 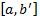 покрывает конечное число интервалов
покрывает конечное число интервалов 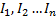 из семейства S, тогда [a, b] покрывает
из семейства S, тогда [a, b] покрывает 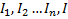 .
.
Лемма доказана.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|