Грани числовых множеств.

Грани числовых множеств.

Множество 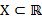называется ограниченным сверху/снизу, если существует такое a, что

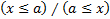
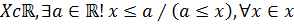
Число, а называется при этом верхней/нижней границей множества. наименьшая верхняя/ наибольшая нижняя граница множества X обозначается sup X/inf X.

Т 7.1

Из определений очевидно, что множество не может иметь более одного супремума или инфинума. Непустое ограниченное сверху снизу множество X имеет единственную верхнюю и нижнюю Грань

Доказательство:

Пусть множество X ограниченное сверху, а Y множество всех верхних границ.

Множество X и Y удовлетворяют всем условиям полноты. Действительно, они не пустые и кроме того для любого и для любого , .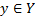

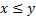На основании всего полноты существует вещественное число ξ:

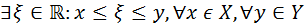первое неравенство показывает, что ξ - верхняя граница для X, а второе - что ξ – наименьшая верхняя граница Y.

Следовательно: ξ =Sup X.

Если бы существовала еще одна верхняя грань для множества X, то .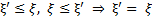

То есть: верхняя грань единственна.

Существование нижней граней и доказательство единственности доказывается аналогично. Теорема доказана

Свойства верхней и нижней граней:

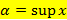
1) 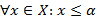(для любого х из Х )

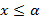2) (для любого )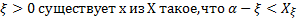

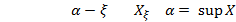
Первое свойство говорит о том, что верхняя грань ( 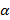) является верхней границей.

Второе свойство говорит о том, что 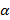нельзя уменьшить.

II.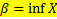

1) 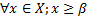(для любого х из Х )

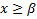2) 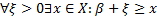(для любого 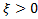существует х из Х такой, что )

Первое свойство говорит о том, что нижняя грань ( 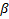) бы является нижней границей.

Второе свойство говорит о том, что 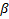нельзя увеличить.

Верхняя и нижняя грани обобщают понятия наибольших и наименьших элементов множества. Если во множестве существует наибольший или наименьший элемент, то он автоматически является верхней или нижней гранью множества.

В дальнейшем условимся считать, что, если множество X не ограничено сверху, то 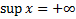, если множество их с неограниченной снизу, то .

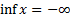В таком случае, любое множество имеет верхнюю или нижнюю грань, при этом: множество, ограниченное сверху, имеет конечную верхнюю грань, а множество ограниченное снизу - конечную верхнюю грань.

12 3 Следующая ⇒