Хелпикс

Главная

Контакты

Случайная статья



Промежутки. Окрестности.. Окрестности.

⇐ ПредыдущаяСтр 2 из 3Следующая ⇒


Промежутки. Окрестности.

Не пустое множество 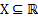 называется промежутком, если для любого .

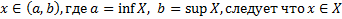Перечислим некоторые часто употребляемые промежутки:

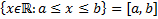 – отрезок .

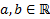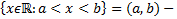интервал .

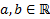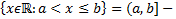интервал, ограниченный слева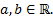

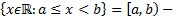интервал, ограниченный справа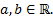

(a - b) – длина промежутка, где a и b – концы.

Кроме конечных промежутков используется также бесконечные промежутки:

.

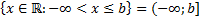
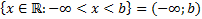
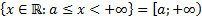
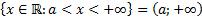
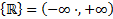Других промежутков во множестве вещественных чисел нет.

Докажем:

Пусть 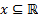 промежуток 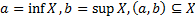, тогда (а, b) ϵ X, что следует из определения промежутка. И мы получим один из вышеперечисленных промежутков, в зависимости от того является ли a и b конечными или бесконечными величинами и в случае когда конец и в случае когда они бесконечные принадлежат они X или нет.

Окрестности.

Близость между вещественными числами можно описывать не только посредством расстояния, но и с помощью окрестностей.

Окрестностью 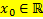 называется любой интервал содержащий эту точку .

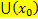Впрочем, обычно рассматриваются симметричные окрестности точки. Под 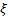 окрестностью точки  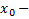интервал ( ).

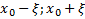Окрестность точки 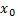это множество точек числовой оси, расположенных от 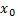на  расстоянии меньше .

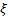Окрестность точки 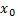без самой точки называют проколотой окрестности точки обозначают Ů( ).

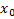Помимо окрестности конечных точек в анализе используется окрестности несобственных точек .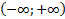

Пусть дано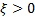

Ů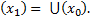

Под E окрестностью символов 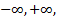а также 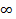условимся понимать бесконечное множество.


1)

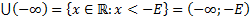
2)

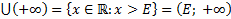
3)

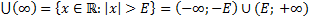
1)  

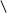
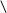
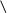
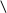
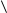
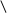
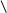
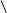
2)

 


3)

 

Несобственные числа не принадлежат своим окрестностям, но тем не менее, точки под их окрестностями не ставятся.


⇐ Предыдущая123Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.