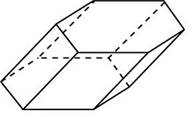
Найдите объем призмы, в основаниях которой лежат правильные шестиугольники со сторонами 2, а боковые ребра равны и наклонены к плоскости основания под углом 30 .

77.66. (№ 27108)Найдите объем призмы, в основаниях которой лежат правильные шестиугольники со сторонами 2, а боковые ребра равны и наклонены к плоскости основания под углом 30 .

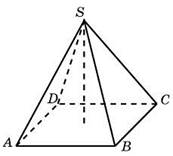
78.67. (№ 27109)В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем.

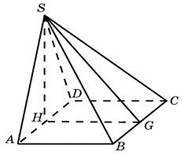
79.68.(№ 27110)Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60 . Высота пирамиды равна 6. Найдите объем пирамиды.

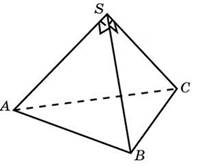
80.69. (№ 27111)Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 3. Найдите объем пирамиды.

81.70.(№ 27112).От призмы 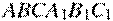, объем которой равен 6, отсечена треугольная пирамида 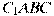. Найдите объем оставшейся части.

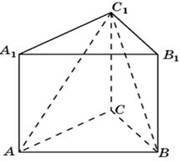
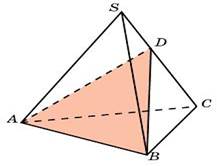
82.71. (№ 27113) Объем треугольной пирамиды SABC, являющейся частью правильной шестиугольной пирамиды SABCDEF, равен 1. Найдите объем шестиугольной пирамиды.

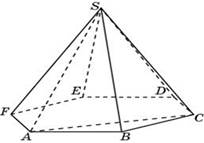
83.72.(№ 27114)Объем правильной четырехугольной пирамиды SABCD равен 12. Точка E — середина ребра SB. Найдите объем треугольной пирамиды EABC.

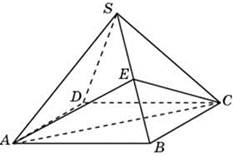
84.73.(№ 27115)От треугольной пирамиды, объем которой равен 12, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.

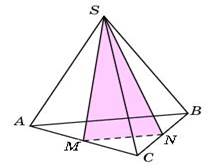
85.74. (№ 27116). Объем треугольной пирамиды равен 15. Плоскость проходит через сторону основания этой пирамиды и пересекает противоположное боковое ребро в точке, делящей его в отношении 1 : 2, считая от вершины пирамиды. Найдите больший из объемов пирамид, на которые плоскость разбивает исходную пирамиду.

86.75.(№ 27117)Найдите объем пространственного креста, изображенного на рисунке и составленного из единичных кубов.

⇐ Предыдущая 123 4 5 Следующая ⇒