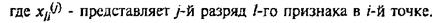Комплексный анализ геоданных при отсутствии эталонных объектов (классификация наблюдений на однородные области)

№10. Комплексный анализ геоданных при отсутствии эталонных объектов (классификация наблюдений на однородные области)

Отсутствие эталонных объектов, на которых проводится оценка статистических характеристик и информативности изучаемых признаков, приводит к необходимости разработки алгоритмов обработки данных комплекса на принципах самообучения. Распознавание образов без обучения на эталонных объектах называется самообучением. При этом число классов и статистические характеристики (распределение) признаков по каждому классу должны быть получены в процессе обработки исходных данных. При распознавании образов без обучения термин "классификация" больше отвечает сущности задачи, поскольку в конечном итоге площадь исследования разделяется на конкретное число однородных по комплексу признаков классов. Геологическая природа таких классов остается неизвестной из-за отсутствия возможности их сравнения с некоторыми эталонами, для ее установления требуется проведение горнобуровых работ. Однако необходимость разбуривания по сети здесь отпадает, так как достаточно бурения одной скважины для каждого класса. Классификация геологических объектов без обучения приобретает особое значение при обработке данных рудной геологии и геофизики в сложно построенных в геологическом отношении районах, когда сложный и непостоянный характер геофизических полей обычно исключает возможность использования эталонных объектов. Среди существующих алгоритмов классификации выделяются: эвристические, использующие различные приемы суммирования (или произведения) признаков; корреляционные, базирующиеся на аппарате компонентного и факторного анализа; статистические, основанные на проверке статистических гипотез.

· Эвристические алгоритмы (использующие различные приемы суммирования (или произведения) признаков). Строятся в предположении о независимости признаков и их одинаковой информативности.В одном из алгоритмов суммирования диапазон значений каждого признака разбивается на заданное и одинаковое по каждому признаку число градаций, например четыре. Результатом суммирования является число

В тех же предположениях о признаках проводится суммирование полных нормированных градиентов, предварительно рассчитанных по методике Березкина для каждого признака в отдельности. Помимо равновесного суммирования признаков, когда равновесность, т. е. равная информативность, обеспечивается делением признаков на одно и то же число разрядов, используются алгоритмы неравновесного суммирования типа

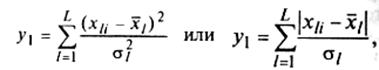
Где Xl и σl2 – соответственно средне значение и дисперсия l-го признака. Для определения порога принятия решения при этом можно использовать критерий χ². При решении частных задач оказываются эффективными алгоритмы типа Yi=X1i*X2i/X3i, для которых не существует математического обоснования и соответственно невозможно оценить величину порога принятия решения.

· Метод главных компонент Корреляционный алгоритм классификации (метод главных компонент) позволяет провести классификацию геологических объектов по зависимым друг от друга признакам и оценивается значимость вклада (весового коэффициента) каждого признака. Чтобы свести задачу обработки данных комплекса признаков для случая разделения объектов на два класса к задаче компонентного анализа, сформулируем принцип классификации следующим образом. Пусть i-й объект относится к классу H1 если выполняется условие 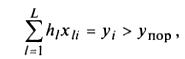(4.17) где yi – комплексный параметр, равный сумме взвешенных значений каждого признака для i-го объекта; h1 – весовой коэффициент l-го признака; yпор – порог принятия решения. Если в рассматриваемом множестве объектов существуют два класса и веса h1 выбраны так, что обеспечивают различные значения yi для этих классов, то вычисление h1 можно свести к процедуре нахождения собственного вектора корреляционной матрицы R исходных признаков, соответствующего ее максимальному собственному числу λmax. Порог для принятия решения о наличии объекта искомого класса определяется на основе центральной предельной теоремы, согласно которой сумма случайных величин распределена нормально. Поэтому величина комплексного параметра yi распределена нормально и порог у_поропределяется заданием вероятности γ:

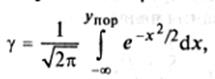где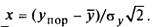

Последовательное вовлечение в обработку новых признаков дает возможность по скорости возрастания комплексного параметра уi судить об их информативности. Выражение (4.17) представляет собой первую главную компоненту, поэтому сам алгоритм реализует вычисление по методу главных компонент. В дальнейшем применение метода главных компонент может идти: путем последовательного нахождения первой главной компоненты раздельно для объектов со значениями у₁ < у_пор и уi, > у_пори т. д.; путем нахождения нескольких (двух-трех) главных компонент, определяющих основную часть дисперсии в пространстве признаков, и их геологического истолкования. Первая главная дампонента выделяет объекты, характеризующиеся наибольшей энергией (дисперсией) в пространстве всех признаков. С целью геологического истолкования нередко оказывается полезной процедура получения нового набора главных компонент (факторов), т.е. вращения факторов.

· Метод К-средних. Пусть множество объектов п следует разбить на заданное число классов М<<n, однородных в смысле заданной метрики классов. Каждый i-й объект описан вектором изучаемых признаков Xli (l= 1,..., n). На первом этапе случайно выбирается к объектов из общей совокупности n объектов (точек наблюдений или ячеек) и в дальнейшем ведется последовательное уточнение этих выбранных, полагаемых эталонными, объектов 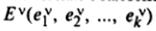c cоответствующим пересчетом приписываемых им весов 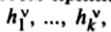, где v-номер итерации, v=0,1,2… Первые случайно расположенные k-объекты являются нулевым приближением , т.е. 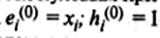, i=1,…,k. Затем извлекается объект (точка) Xk+1 и выясняется, к какому из эталонов ei(0) он оказался ближе всего. Этот эталон заменяется новым, определяемым как "центр тяжести" старого эталона и присоединенного к нему объекта Xk+1 с увеличением на единицу соответствующего ему веса. Пересчет эталонов и соответствующих им весов на v-м шаге проводится согласно формулам

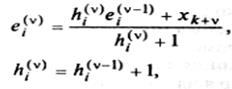
при условии, что среднеквадратическое расстояние между Xk+v и eiv-1 минимально, т.е. p(Xk+v, eiv-1) = min p(Xk+v,ejv-1), j=1,…,k и по формулам ei(v) = hiev-1, hi(v)=hi(v-1) если это условие не выполняется.

После уточнения эталонной совокупности проводится окончательная классификация множества объектов п по комплексу признаков с целью выделения М классов в соответствии с правилом минимального дистанционного разбиения относительно "центров тяжести" (эталонных объектов) классов, т. е. 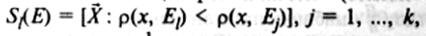j≠0. Это разбиение – наилучшее в смысле функционала качества

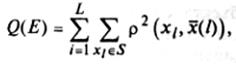
Который является взвешенной суммой внутриклассовых дисперсий.

⇐ Предыдущая 4 5 6 7 8910 11 12 13 Следующая ⇒