Надёжность обнаружения сигналов и её использование для выбора информативности геофизических методов (признаков)

№7. Надёжность обнаружения сигналов и её использование для выбора информативности геофизических методов (признаков)

Надежность – γ, наиболее универсальная оценка информативности как отдельно взятого признака (поля), так и сочетаний (комплекса) признаков (полей). Надежность разделения объектов двух классов, определяемую по разности площадей под гистограммами распределений признака S₁ и S₂, построенными для объектов классов Н₁ и Н₂: γ=1-q; где q= 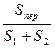. Здесь q – вероятность ошибки разделения классов Н₁ и Н₂, равная q=р₁α+р₂β. Здесь р₁ и р₂ – априорные вероятности появления объектов классов Н₁ и Н₂. Обычно р₁=р₂=0,5, α – ошибка первого рода (предлагают наличие Н₂, а на самом деле Н₁). Величина β – вероятность ошибки второго рода (наоборот).

Надежность разделения объектов двух классов по комплексу L признаков определяется как

Выражение (4.8) может быть использовано для оценки информативности, т. е. надежности разделения объектов, по любому сочетанию признаков. По максимальной величине γ_комп устанавливается информативная совокупность признаков. Такой совокупностью обеспечивается выбор наиболее эффективного в смысле оценки геологической природы источников аномалий комплекса геофизических методов.

Величина надежности задается в зависимости от поставленной задачи (например, поиски только крупных или крупных и средних месторождений и т. п.) и должна составлять примерно 97,0 - 99,5%. Значение надежности, равное 99,5%, получается из условия того, что аномалия фиксируется тремя точками (т = 3), каждая из которых по интенсивности превышает трехкратный уровень помех.
№8. Принципы комплексного анализа геоданных

Целью комплексного анализа геоданных является достижение однозначности геологического истолкования геофизических полей. При этом под КА понимается обработка комплекса различных признаков, при которой обычно решаются задачи геокартирования и районирования исследуемой площади (или разреза) на несколько классов, охарактеризованных тем или иным набором признаков. КА обеспечивает качественную интерпретацию по оценке природы источников.

В настоящее время существует 2 основных подхода к обработке и интерпретации результатов геофизических съемок: детерминированный и вероятностно-статистический.

Первый базируется на аналитических методах теории потенциала (гравиразведка, магниторазведка, терморазведка, электроразведка постоянным током и ЕП), уравнений Максвелла (ЭМ методы) и теории упругости (сейсморазведка).

Использование ВС подхода обусловлено характерной особенностью геофизических наблюдений, заключающееся в том, что полученные в отдельных точках данные следует рассматривать как случайные величины. Случайно также расположение изучаемых геологических объектов, точек и даже площадей исследования, поскольку при съемке другими исполнителями и в другое время могут изменятся контуры площади и расположение сетей наблюдений, а из-за наложений помех, вызванных погрешностями измерений, геологическими неоднородностями ВЧР, неучтенными вариациями полей и другими причинами, само физическое поле реализуется случайным образом. Следовательно, для выделения слабоконтрастных, малоразмерных или залегающих на больших глубинах объектов необходимо применение методов теории вероятностей, математической статистики и случайных процессов.

В общем виде задачу комплексной интерпретации можно представить как математическую модель:

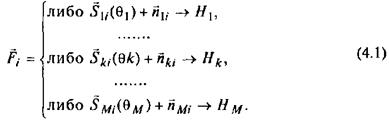
Здесь – вектор значений L различных полей и признаков этих полей, 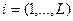; индекс к (K=1,…,M) характеризует различные по геологической природе объекты исследований; М- общее число классов объектов, или число статистических гипотез H₁,H₂,…,H_M.

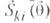неслучайная, аномальная компонента i-го поля (признака), зависящая от вектора параметров искомого объекта 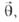который включает физические свойства, геометрию и форму объекта. При детерминированном подходе 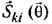находится из решения прямой задачи; 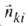- случайная компонента (помеха) для того же i-го поля (признака).

При комплексном анализе геофизических данных в модели (4.1) достаточно ограничиться суммой 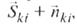т. е. без учета вектора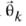

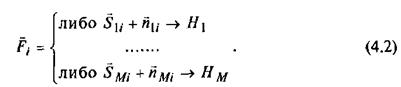
Когда в модели (4.2) предполагается наличие априорной информации о числе классов М и о статистических характеристиках каждого поля (признака) для этих классов, то задача комплексного анализа сводится к распознаванию образов с предварительным обучением на эталонных объектах. В том случае, когда число классов неизвестно и нет информации о статистических характеристиках, задача комплексного анализа сводится к задаче классификации (распознавание образов без обучения или самообучение) на некоторое, априори не известное число однородных (по совокупности признаков) классов. При этом как число классов, так и статистические характеристики признаков оцениваются в процессе обработки исходных данных.

⇐ Предыдущая 2 3 4 5 678 9 10 11 Следующая ⇒