
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
ИНТЕГРАЛЫ С БЕСКОНЕЧНЫМИ ПРЕДЕЛАМИ ИНТЕГРИРОВАНИЯ
Если функция 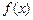 собственно интегрируема либо в промежутках
собственно интегрируема либо в промежутках  (при любых
(при любых 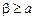 ), либо в промежутках
), либо в промежутках 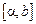 (при любых
(при любых 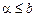 ), либо как в первых, так и во вторых промежутках, то для каждого из этих случаев по определению несобственных интегралов, соответственно имеем:
), либо как в первых, так и во вторых промежутках, то для каждого из этих случаев по определению несобственных интегралов, соответственно имеем:
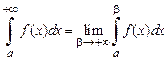 ,
, 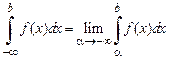 ,
,
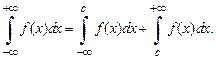 (*)
(*)
Если 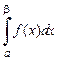 при
при 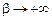 имеет конечный предел, то говорят, что в этом случае несобственный интеграл
имеет конечный предел, то говорят, что в этом случае несобственный интеграл  существует или сходится.
существует или сходится.
Если 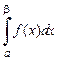 при
при 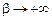 не имеет конечного предела, то говорят, что в этом случае несобственный интеграл
не имеет конечного предела, то говорят, что в этом случае несобственный интеграл  не существует или расходится.
не существует или расходится.
Аналогичным образом определяются понятия сходимости или расходимости интеграла 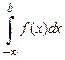 .
.
Равенство 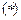 означает, что если каждый из несобственных интегралов, стоящих в правой части его, существует (сходится), то существует (сходится) и несобственный интеграл, стоящий в левой части равенства.
означает, что если каждый из несобственных интегралов, стоящих в правой части его, существует (сходится), то существует (сходится) и несобственный интеграл, стоящий в левой части равенства.
В противном случае, если хотя бы один из интегралов, стоящих в правой части равенства 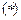 , будет расходящимся, то будет расходиться и интеграл
, будет расходящимся, то будет расходиться и интеграл 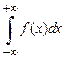 .
.
ИНТЕГРАЛЫ ОТ НЕОГРАНИЧЕННЫХ НА ОТРЕЗКЕ
[a, b] ФУНКЦИЙ
Если функция 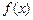 имеет бесконечный разрыв при
имеет бесконечный разрыв при 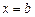 и собственно интегрируема на отрезках
и собственно интегрируема на отрезках 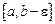 при любых как угодно малых
при любых как угодно малых 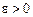 , то по определению несобственного интеграла (для данного случая) имеем:
, то по определению несобственного интеграла (для данного случая) имеем:
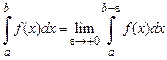 .
.
Если функция 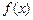 имеет бесконечный разрыв при
имеет бесконечный разрыв при 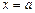 и собственно интегрируема на отрезках
и собственно интегрируема на отрезках 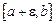 при любых как угодно малых
при любых как угодно малых 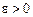 , то по определению несобственного интеграла (для данного случая) имеем:
, то по определению несобственного интеграла (для данного случая) имеем:
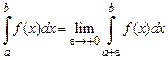 .
.
Если функция 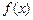 имеет бесконечный разрыв при
имеет бесконечный разрыв при 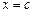 ,
, 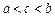 , и непрерывна при
, и непрерывна при 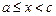 и
и 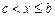 , то несобственный интеграл представляется в виде:
, то несобственный интеграл представляется в виде:
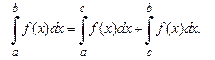 (**)
(**)
Если 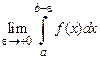 существует, то несобственный интеграл
существует, то несобственный интеграл 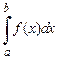 от функции
от функции 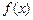 , имеющей бесконечный разрыв в точке
, имеющей бесконечный разрыв в точке 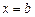 , существует и сходится, в противном случае говорят, что несобственный интеграл
, существует и сходится, в противном случае говорят, что несобственный интеграл 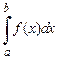 расходится.
расходится.
Аналогично решается вопрос о сходимости или расходимости несобственного интеграла 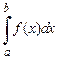 от функции, имеющей бесконечный разрыв на левом конце промежутка интегрирования, т. е. при
от функции, имеющей бесконечный разрыв на левом конце промежутка интегрирования, т. е. при 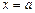 .
.
Равенство 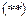 представляет несобственный интеграл от функции, имеющей бесконечный разрыв в некоторой внутренней точке
представляет несобственный интеграл от функции, имеющей бесконечный разрыв в некоторой внутренней точке 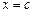 отрезка интегрирования
отрезка интегрирования 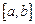 , в виде суммы двух несобственных интегралов от функции, имеющей бесконечный разрыв лишь на одном из концов отрезка интегрирования, определение которых дано выше.
, в виде суммы двух несобственных интегралов от функции, имеющей бесконечный разрыв лишь на одном из концов отрезка интегрирования, определение которых дано выше.
Если оба несобственных интеграла, стоящих в правой части формулы 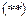 , существуют (сходятся), то существует (сходится) и несобственный интеграл, стоящий в левой части этой формулы.
, существуют (сходятся), то существует (сходится) и несобственный интеграл, стоящий в левой части этой формулы.
В противном случае, если хотя бы один из интегралов, стоящих в правой части равенства 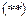 ,будет расходящимся, то будет расходиться и интеграл
,будет расходящимся, то будет расходиться и интеграл 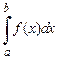 , стоящий в левой части этого равенства.
, стоящий в левой части этого равенства.
ПРИЗНАКИ СХОДИМОСТИ И РАСХОДИМОСТИ
НЕСОБСТВЕННЫХ ИНТЕГРАЛОВ
1. Если в результате замены переменной интегрирования несобственный интеграл представляется в виде интеграла, существующего в собственном смысле, то тогда и исходный несобственный интеграл существует, т. е. является сходящимся.
2. Применение основной формулы интегрального исчисления (формулы Ньютона–Лейбница)
Если первообразная 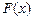 для подынтегральной функции
для подынтегральной функции 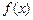 имеет конечный предел при предельном переходе, используемом в определении несобственного интеграла того или иного типа, то соответствующий интеграл сходится. В противном случае несобственный интеграл расходится.
имеет конечный предел при предельном переходе, используемом в определении несобственного интеграла того или иного типа, то соответствующий интеграл сходится. В противном случае несобственный интеграл расходится.
Например:
а) если 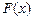 – первообразная для функции
– первообразная для функции 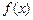 и существует конечный предел
и существует конечный предел  , то интеграл
, то интеграл  сходится и равен
сходится и равен
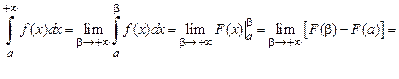
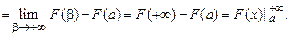
Тем самым показывается, что и для несобственного интеграла этого типа в таком случае оказывается справедливой формула Ньютона–Лейбница;
б) если 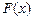 – первообразная для функции
– первообразная для функции 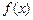 , неограниченной в окрестности точки
, неограниченной в окрестности точки 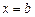 , и существует конечный предел
, и существует конечный предел 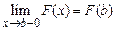 , то несобственный интеграл
, то несобственный интеграл 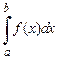 сходится и равен
сходится и равен
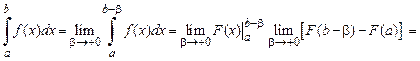
= 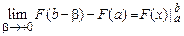 .
.
Тем самым показывается, что и для несобственного интеграла этого типа в таком случае оказывается справедливой формула Ньютона–Лейбница.
Аналогично выше приведенным примерам формула Ньютона–Лейбница может быть применена при вычислении и других типов несобственных интегралов (или при установлении их расходимости) в случае существования (или несуществования) конечных пределов первообразной для подынтегральной функции при соответствующих предельных переходах.
3. Непосредственно применяя формулу Ньютона–Лейбница, легко получить, что:
а) 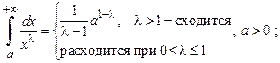
б) 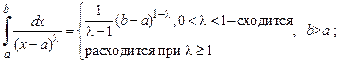
в) 
4. Признаки сравнения для положительных подынтегральных функций
При формулировке признаков сравнения и следующего за ними предельного признака сравнения под промежутком интегрирования 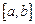
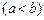 мы подразумеваем как конечный промежуток, так и бесконечный, т. е.
мы подразумеваем как конечный промежуток, так и бесконечный, т. е. 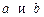 могут быть как конечными числами, так и бесконечностями с соответствующим знаком; также, говоря об особой точке сравниваемых подынтегральных функций, мы подразумеваем под ней либо конечную точку, в которой сравниваемые функции терпят бесконечный разрыв, либо бесконечно удаленную точку. Кроме того, под предельным переходом
могут быть как конечными числами, так и бесконечностями с соответствующим знаком; также, говоря об особой точке сравниваемых подынтегральных функций, мы подразумеваем под ней либо конечную точку, в которой сравниваемые функции терпят бесконечный разрыв, либо бесконечно удаленную точку. Кроме того, под предельным переходом 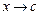 (где
(где 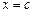 – особая точка: либо
– особая точка: либо  , либо
, либо 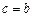 ) мы подразумеваем тот односторонний предельный переход, который используется в определении исследуемого на сходимость несобственного интеграла, т. е. либо
) мы подразумеваем тот односторонний предельный переход, который используется в определении исследуемого на сходимость несобственного интеграла, т. е. либо 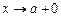 (
(  ), либо
), либо 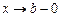 (
( 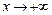 ).
).
С учетом этого замечания признаки сравнения для положительных подынтегральных функций в общем случае могут быть сформулированы следующим образом:
Теорема сравнения I. Если в окрестности особой точки имеет место неравенство 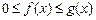 , то:
, то:
а) из сходимости несобственного интеграла 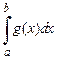 следует сходимость несобственного интеграла
следует сходимость несобственного интеграла 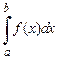 ;
;
б) из расходимости несобственного интеграла 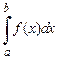 следует расходимость несобственного интеграла
следует расходимость несобственного интеграла 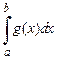 .
.
Теорема сравнения II. (Предельный признак сравнения):
а) если существует предел

то несобственные интегралы 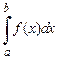 и
и 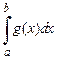 сходятся или расходятся одновременно;
сходятся или расходятся одновременно;
б) в частности, если 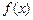 ~
~ 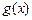 при
при 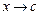 , то
, то 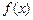 и
и 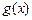 одновременно либо интегрируемы, либо неинтегрируемы на промежутке
одновременно либо интегрируемы, либо неинтегрируемы на промежутке 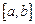 .
.
Замечание: относительно предельного перехода 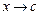 , фигурирующего в этом предельном признаке сравнения, смотрите замечание, приведенное в начале предыдущего пункта, где приведены непредельные признаки сравнения.
, фигурирующего в этом предельном признаке сравнения, смотрите замечание, приведенное в начале предыдущего пункта, где приведены непредельные признаки сравнения.
5. Признаки Коши (для положительных подынтегральных функций).
I. Пусть для достаточно больших 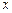 функция
функция 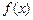 имеет вид
имеет вид 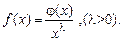 Тогда:
Тогда:
1) если 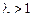 и
и 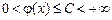 , то интеграл
, то интеграл  сходится,
сходится,
2) если  и
и 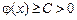 , то интеграл
, то интеграл  расходится.
расходится.
Более удобная для практики частная форма сформулированных признаков Коши, такова:
если при 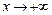 функция
функция 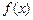 является бесконечно малой порядка
является бесконечно малой порядка 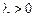 по сравнению с
по сравнению с 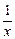 , то интеграл
, то интеграл  сходится или расходится в зависимости от того, будет ли,
сходится или расходится в зависимости от того, будет ли, 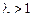 или
или  .
.
II. Пусть для достаточно близких к 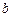 (либо к
(либо к 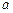 ) значений
) значений 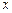 функция
функция 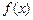 имеет вид
имеет вид
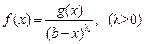 ,
, 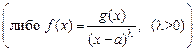 .
.
Тогда:
1) если 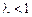 и
и  , то несобственный интеграл
, то несобственный интеграл 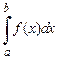 сходится,
сходится,
2) если 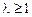 и
и 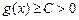 , то несобственный интеграл
, то несобственный интеграл 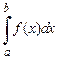 расходится.
расходится.
Более удобная для практики частная форма сформулированных признаков Коши, такова:
если при 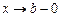 (при
(при 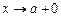 ) функция
) функция 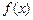 является бесконечно большой порядка
является бесконечно большой порядка 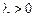 по сравнению с
по сравнению с 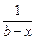
(по сравнению с  ), то несобственный интеграл
), то несобственный интеграл 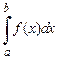 сходится или расходится в зависимости от того, будет ли соответственно
сходится или расходится в зависимости от того, будет ли соответственно 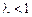 или
или 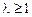 .
.
6. Абсолютная сходимость несобственных интегралов.
Если сходится в промежутке интегрирования 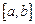 (конечном или бесконечном) несобственный интеграл
(конечном или бесконечном) несобственный интеграл 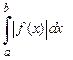 от
от 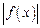 , то сходится и несобственный интеграл
, то сходится и несобственный интеграл 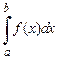 от самой функции
от самой функции 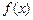 , при этом несобственный интеграл
, при этом несобственный интеграл 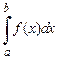 называется абсолютно сходящимся, а сама функция
называется абсолютно сходящимся, а сама функция 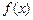 – абсолютно интегрируемой в
– абсолютно интегрируемой в 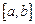 .
.
Так как  то при установлении абсолютной сходимости несобственных интегралов можно пользоваться признаками сравнения, предельным признаком сравнения и признаками Коши, сформулированными для положительных подынтегральных функций.
то при установлении абсолютной сходимости несобственных интегралов можно пользоваться признаками сравнения, предельным признаком сравнения и признаками Коши, сформулированными для положительных подынтегральных функций.
Если функция 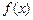 абсолютно интегрируема в промежутке
абсолютно интегрируема в промежутке 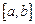 (конечном или бесконечном), а функция
(конечном или бесконечном), а функция 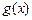 ограничена в этом промежутке, то и произведение
ограничена в этом промежутке, то и произведение 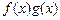 будет функцией абсолютно интегрируемой в промежутке
будет функцией абсолютно интегрируемой в промежутке 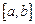 .
.
РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ
Задача 1.Вычислить определенный интеграл 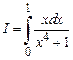 .
.
Решение (интегрирование подведением под знак дифференциала).
Представим подынтегральное выражение в виде произведения двух функций 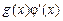 , где
, где 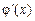 имеет очевидную первообразную
имеет очевидную первообразную 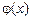 , а
, а 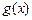 есть функция этой первообразной:
есть функция этой первообразной: 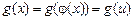 ,
, 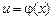 , т. е.
, т. е.
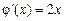 ,
, 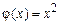 ,
, 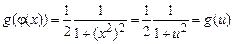 ,
,
но 
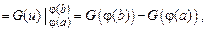
тогда
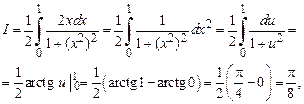
где  .
.
Ответ. 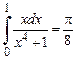 .
.
Задача 2. Вычислить определенный интеграл 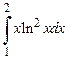 .
.
Решение(интегрирование по частям).
Представим подынтегральное выражение в виде произведения двух функций  , где
, где  имеет очевидную первообразную
имеет очевидную первообразную 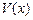 , а
, а 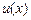 – дифференцируемая функция, причем ее производная
– дифференцируемая функция, причем ее производная 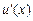 является более простой функцией, чем
является более простой функцией, чем 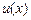 .
.
В данном случае 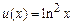 ,
, 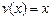 ,
, 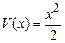 ,
, 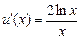 . Применим формулу интегрирования по частям:
. Применим формулу интегрирования по частям:
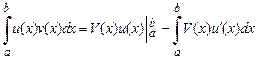 ,
,
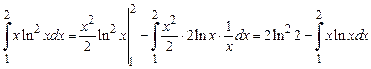 .
.
Последний интеграл не является табличным, но к нему можно повторно применить формулу интегрирования по частям. Теперь
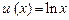 ,
, 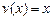 ,
, 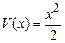 ,
,  ,
,
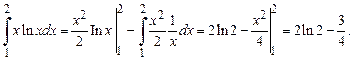
Ответ.  .
.
Задача 3. Вычислить определенный интеграл
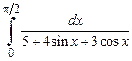 .
.
Решение (интегрирование выражений 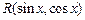 ).
).
Поскольку функция 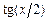 определена на
определена на 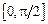 , сделаем универсальную тригонометрическую подстановку
, сделаем универсальную тригонометрическую подстановку  . Подставляя в подынтегральное выражение
. Подставляя в подынтегральное выражение
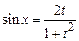 ;
; 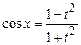 ;
;  ,
,
получим 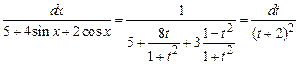 .
.
Находим новые пределы интегрирования 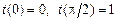 . Применим формулу замены переменной в определенном интеграле:
. Применим формулу замены переменной в определенном интеграле:

Ответ.  .
.
Задача 4. Вычислить определенный интеграл
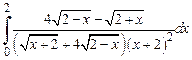 .
.
Решение(интегрирование выражений
 ).
).
Чтобы сделать подстановку, приводящую к интегралу от рациональной функции, нужно преобразовать подынтегральную функцию так, чтобы она содержала корни любой степени, но из одного и того же выражения вида 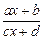 . Поэтому преобразуем подынтегральное выражение, выделяя
. Поэтому преобразуем подынтегральное выражение, выделяя 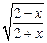 , затем применим подстановку
, затем применим подстановку 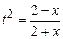 ,
, 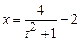 ,
, 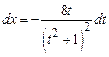 ,
, 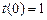 ,
, 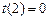 :
:
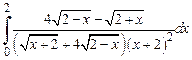 =
= 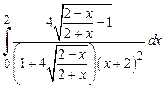 =
=

Ответ. 
Задача 5. Вычислить определенный интеграл 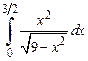 .
.
Решение(интегрирование выражений 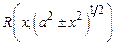 и
и
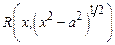 ).
).
Для избавления от радикала используют тригонометрические или гиперболические подстановки. В данном случае применим подстановку 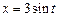 . Тогда
. Тогда
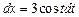 ,
, 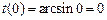 ,
, 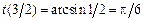 ,
,
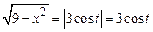 , поскольку
, поскольку 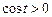 при
при  .
.
Сделаем замену переменной в определенном интеграле:
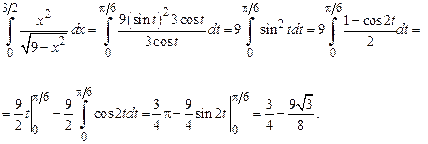
Ответ. 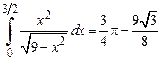 .
.
Задача 6. Оценить интеграл 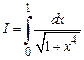 .
.
Решение. Имеем:  при
при 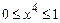 , тогда
, тогда 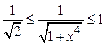 , т. е. согласно теореме об оценке определенного интеграла
, т. е. согласно теореме об оценке определенного интеграла 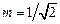 ,
, 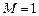 ,
, 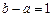 . Следовательно,
. Следовательно, 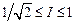 . Ответ.
. Ответ.  .
.
Задача 7. Оценить интеграл 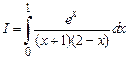 .
.
Решение. Воспользуемся обобщенной теоремой об оценке определенного интеграла. Пусть 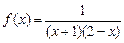 ,
,  .
.
Производная  обращается в нуль при
обращается в нуль при 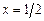 и меняет знак в этой точке с минуса на плюс. Следовательно, функция
и меняет знак в этой точке с минуса на плюс. Следовательно, функция 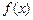 имеет в этой точке минимум. Максимума функция
имеет в этой точке минимум. Максимума функция 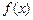 достигает на концах отрезка
достигает на концах отрезка 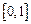 и
и 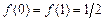 . Таким образом,
. Таким образом, 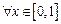 выполняется система неравенств:
выполняется система неравенств: 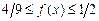 , а при
, а при 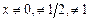 строгие неравенства:
строгие неравенства: 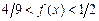 . Поэтому, применяя обобщенную теорему об оценке определенного интеграла, получим:
. Поэтому, применяя обобщенную теорему об оценке определенного интеграла, получим:
 или, окончательно,
или, окончательно,  .
.
Ответ.  .
.
Задача 8. Найти 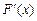 , если
, если  .
.
Решение. Функции 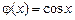 и
и 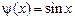 определены, непрерывны, а следовательно, дифференцируемы
определены, непрерывны, а следовательно, дифференцируемы  . Причем
. Причем 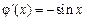 и
и 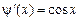 . Тогда согласно теореме о дифференцировании определенного интеграла имеем:
. Тогда согласно теореме о дифференцировании определенного интеграла имеем:

Ответ. 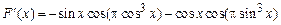 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|