
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Предисловие. Список рекомендуемой литературы. ЧАСТЬ I. ВЫЧИСЛЕНИЯ ОПРЕДЕЛЕННЫХ. И НЕСОБСТВЕННЫХ ИНТЕГРАЛОВ. СПРАВОЧНЫЙ МАТЕРИАЛ
Предисловие
Данный типовой расчет состоит из трех частей:
1) вычисления определенных и несобственных интегралов;
2) геометрические приложения определенных интегралов;
3) физические приложения определенных интегралов, приближенное вычисление определенных интегралов.
В каждой части типового расчета приводится справочный материал, который можно использовать при выполнении расчетных заданий, примеры решения типовых задач, варианты индивидуальных заданий.
Приведен список рекомендованной литературы.
В справочный материал данного типового расчета помещены основные определения и математические факты, непосредственно касающиеся задач, приведенных в индивидуальных заданиях.
Список рекомендуемой литературы
1. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. – М.: Наука, 1963, 1966. – Т. 2, 3.
2. Демидович Б.Н. Сборник задач и упражнений по математическому анализу. – М.: Изд-во «АСТ», 2007.
3. Ильин В.А., Садовничий В.А., Сендов В.Х. Математический анализ. Ч.1 – М.: Юрайт, 2013.
4. Убодоев В.В., Иринчеев А.А., Макунина Т.А., Телешева Л.А. Математический анализ: неопределенный и определенный интеграл. – Улан-Удэ: Изд-во Бурятского госуниверситета, 2010.
5. Ошоров Б.Б. Одномерный математический анализ: Учебное пособие. – Улан-Удэ: Изд-во ВСГТУ, 2009.
ЧАСТЬ I
ВЫЧИСЛЕНИЯ ОПРЕДЕЛЕННЫХ
И НЕСОБСТВЕННЫХ ИНТЕГРАЛОВ
СПРАВОЧНЫЙ МАТЕРИАЛ
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ (в смысле Римана)
Если функция 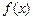 определена на конечном отрезке
определена на конечном отрезке 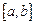 и
и 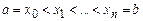 – произвольное разбиение отрезка
– произвольное разбиение отрезка 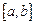 на элементарные отрезки
на элементарные отрезки 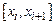 , (
, ( 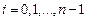 ), то определенным интегралом (в собственном смысле) от функции
), то определенным интегралом (в собственном смысле) от функции 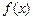 на отрезке
на отрезке 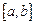 называется число (если оно существует)
называется число (если оно существует)
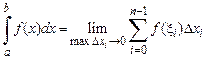 ,
,
где 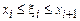 (произвольное) и
(произвольное) и 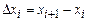 .
.
Функции 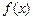 , для которых упомянутый выше предел существует, называются интегрируемыми (собственно) на отрезке
, для которых упомянутый выше предел существует, называются интегрируемыми (собственно) на отрезке 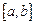 . В частности:
. В частности:
а) непрерывная на 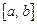 функция;
функция;
б) ограниченная на 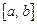 функция, имеющая на этом отрезке конечное число точек разрыва;
функция, имеющая на этом отрезке конечное число точек разрыва;
в) ограниченная монотонная на 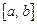 функция (которая может иметь в этом промежутке и бесконечное число точек разрыва);
функция (которая может иметь в этом промежутке и бесконечное число точек разрыва);
– интегрируемы на любом конечном отрезке 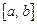 .
.
Если функция 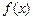 не ограничена на отрезке
не ограничена на отрезке 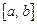 , то она собственно (т. е. в собственном смысле) не интегрируема на
, то она собственно (т. е. в собственном смысле) не интегрируема на 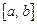 .
.
ОСНОВНЫЕ СВОЙСТВА ОПРЕДЕЛЕННОГО
ИНТЕГРАЛА
1. Постоянный множитель можно выносить за знак определенного интеграла:
если 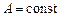 , то
, то 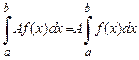 .
.
2. Определенный интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме интегралов от каждой из слагаемых функций:
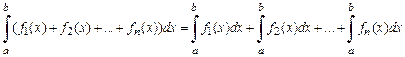 .
.
3. При перемене местами нижнего и верхнего пределов интегрирования определенный интеграл изменяет знак на обратный (его абсолютная величина при этом не изменяется):
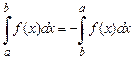 ,
,
отсюда следует, что
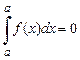 .
.
4. Для любых трех чисел 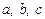 справедливо равенство
справедливо равенство
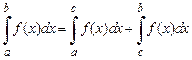 ,
,
если все три интеграла существуют.
5. Если 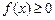 на отрезке
на отрезке 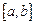 ,
, 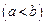 , то
, то 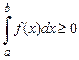 .
.
6. Если 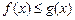 на отрезке
на отрезке 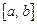 ,
, 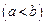 , то
, то
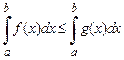 .
.
7. 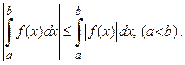
8. Теорема об оценке определенного интеграла. Если:
а) 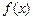 интегрируема на
интегрируема на 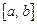 ,
, 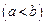 ,
,
б) во всем этом промежутке 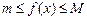 , то
, то
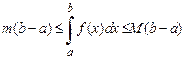 .
.
9. Обобщенная теорема об оценке определенного интеграла. Если:
а) 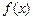 и
и 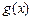 интегрируемы на
интегрируемы на 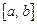 ,
, 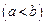 ,
,
б) во всем этом промежутке 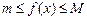 ,
,
в) 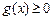 на
на 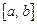 , то
, то
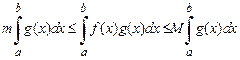 .
.
10. Теорема о среднем. Пусть:
а) 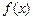 интегрируема на
интегрируема на 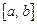 ,
, 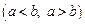 ,
,
б) во всем этом промежутке 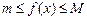 , тогда
, тогда
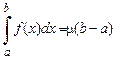 ,
,
где 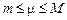 (
( 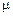 – среднее значение функции
– среднее значение функции 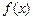 на
на 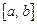 ).
).
Если, кроме того, функция 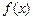 непрерывна на
непрерывна на 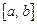 , то
, то 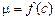 , где
, где 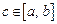 , т. е.
, т. е.
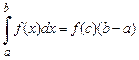 .
.
11. Обобщенная теорема о среднем. Пусть:
а) 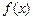 и
и 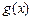 интегрируемы на
интегрируемы на 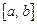 ,
, 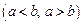 ,
,
б) во всем этом промежутке 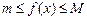 ,
,
в) 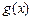 на
на 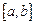 не меняет знака:
не меняет знака: 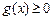 (
( 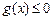 ), тогда
), тогда
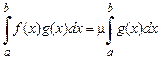 ,
,
где 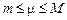 (
( 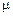 – среднее значение функции
– среднее значение функции 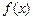 на
на 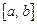 ).
).
Если к тому же функция 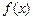 непрерывна на
непрерывна на 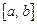 , то
, то 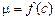 , где
, где 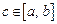 , т. е.
, т. е.
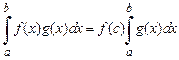 .
.
ТЕОРЕМА О ДИФФЕРЕНЦИРОВАНИИ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Если: а) 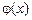 и
и 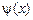 дифференцируемы в точке
дифференцируемы в точке 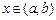 ,
,
б) 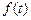 непрерывна хотя бы в как угодно малой окрестности точки
непрерывна хотя бы в как угодно малой окрестности точки 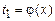 и
и 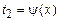
 и интегрируема в промежутке
и интегрируема в промежутке 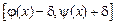 (
( 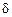 – как угодно малое число), то
– как угодно малое число), то
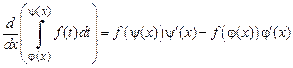 .
.
В частности, если 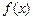 непрерывна на
непрерывна на 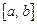 , то
, то 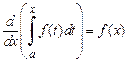 ,
, 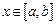 , т. е.
, т. е. 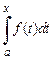 с переменным верх –
с переменным верх –
ним пределом является одной из первообразных функций 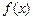 , именно той первообразной, которая обращается в нуль при
, именно той первообразной, которая обращается в нуль при 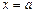 , так как
, так как
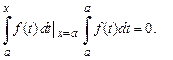
ФОРМУЛА НЬЮТОНА–ЛЕЙБНИЦА
Если функция определена и непрерывна на отрезке 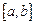 , и
, и 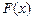 ее первообразная, т. е.
ее первообразная, т. е. 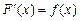 , то
, то
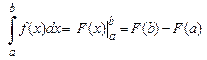 .
.
ТЕОРЕМА ОБ ИНВАРИАНТНОСТИ ФОРМУЛ НЕОПРЕДЕЛЕННОГО ИНТЕГРИРОВАНИЯ
(Следует из теоремы об инвариантности формы первого дифференциала функции.)
Всякая формула неопределенного интегрирования сохраняет свой вид при подстановке вместо независимой переменной любой дифференцируемой функции от нее, т. е. если 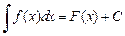 , то и
, то и 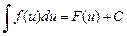 , где
, где 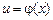 –любая дифференцируемая функция от
–любая дифференцируемая функция от 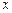 .
.
Из этой теоремы следует следующий метод замены переменной в определенном интеграле в форме, в которой этот метод еще называется методом подведения под знак дифференциала.
ЗАМЕНА ПЕРЕМЕННОЙ В ОПРЕДЕЛЕННОМ
ИНТЕГРАЛЕ
Метод подведения под знак дифференциала
Пусть: а) функции 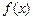 ,
, 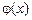 ,
, 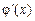 ,
, 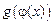 –непрерывные функции на отрезке
–непрерывные функции на отрезке 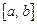 , б)
, б) 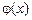 – монотонная функция.
– монотонная функция.
Тогда, если подынтегральное выражение 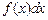 в интеграле
в интеграле 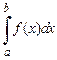 удается записать в виде
удается записать в виде 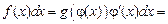
= 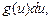 где
где 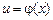 (новая переменная выражается через старую), и первообразная
(новая переменная выражается через старую), и первообразная 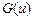 функции
функции 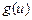 может быть нами сравнительно просто найдена, то
может быть нами сравнительно просто найдена, то
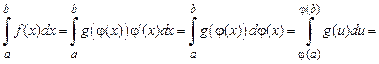
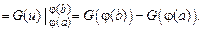
Метод подстановки
Можно производить замену переменной в определенном интеграле, выражая не новую переменную 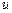 через старую переменную
через старую переменную 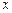 (как в предыдущем случае), а наоборот, выражая старую переменную
(как в предыдущем случае), а наоборот, выражая старую переменную 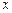 через новую переменную
через новую переменную 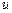 .
.
Для этого сформулируем следующее правило:
Если в промежутке 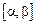 функции
функции 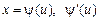 и
и 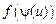 непрерывны и
непрерывны и 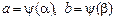 , то
, то
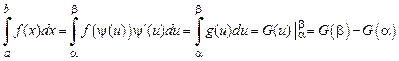 .
.
ИНТЕГРИРОВАНИЕ ПО ЧАСТЯМ
Если 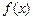 ,
, 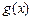 ,
, 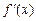 и
и 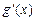 – непрерывные функции на отрезке
– непрерывные функции на отрезке 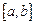 , то
, то
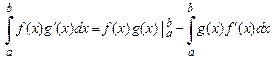 ,
,
здесь 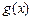 – любая первообразная функции
– любая первообразная функции 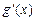 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|