
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задача №2. Решение.. Задача №3 . Решение.. Задача №4 . Решение.. Решение задач на вычисление объёма цилиндра.. Задача №5 . Решение.
Задача №2
Радиус основания цилиндра равен 5 см, а его образующая – 9 см. Найдите площадь осевого сечения.
Дано: цилиндр, ABCD – осевое сечение.
AO=5cм.
AB=9см.
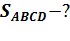
Решение.
Данное осевое сечение есть прямоугольник ABCD. Сторона прямоугольника AD=2*5 =10см.
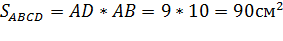
Ответ: 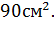
Задача №3
Прямоугольник, стороны которого равны 6 см и 4 см, вращается около меньшей стороны. Найдите площадь поверхности тела вращения.
Дано: ABCD – прямоугольник, AВ = 6 см, BС = 4см,
ВC – ось вращения.
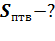
Решение.
Данное тело вращения – прямой круговой цилиндр с высотой BC = 4 см и радиусом основания АВ = 6 см.
Площадь полной поверхности цилиндра вычисляется по формуле:
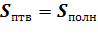 =
= 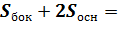 2πRh+2π
2πRh+2π 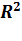 =2πR⋅(h+R)=2π*6*(4+6)=120π
=2πR⋅(h+R)=2π*6*(4+6)=120π  )
)
Ответ: 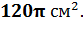
Задача №4
Длина окружности основания прямого цилиндра С = 10м, длина образующей l = 7м. Чему равна площадь боковой поверхности цилиндра?
Дано: прямой цилиндр.
C=10м.
l=7м.
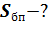
Решение.
Площадь боковой поверхности цилиндра равна произведению длины окружности его основания на высоту: 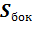 =2πR⋅H=С*H. Высота цилиндра равна его образующей: H=l= 7м. Поэтому
=2πR⋅H=С*H. Высота цилиндра равна его образующей: H=l= 7м. Поэтому 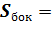 10*7=70
10*7=70 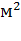
Ответ: 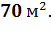
2. Решение задач на вычисление объёма цилиндра.
Задача №5
Объем цилиндра равен 64π, а площадь боковой поверхности равна 32π. Найдите площадь полной поверхности цилиндра, деленную на π.
Решение.
Объём цилиндра вычисляется по формуле: 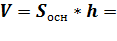 π
π 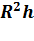 ,а площадь боковой поверхности
,а площадь боковой поверхности 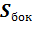 =2πRh.
=2πRh.
Зная величину объема и боковой поверхности, можно выразить радиус цилиндра:
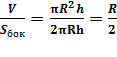 =
= 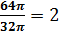 ,R=4.
,R=4.
Площадь полной поверхности складывается из площади боковой поверхности и площадей двух оснований: 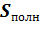 =
= 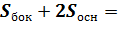 2πRh+2π
2πRh+2π 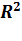 =32
=32 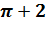 π*16=64
π*16=64 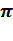
Необходимо найти площадь полной поверхности цилиндра, деленную на π, т.е.
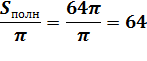
Ответ: 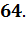
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|