
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Для того чтобы построить график , нужно часть исходного графика, лежащую выше оси , оставить без изменения, а нижнюю отразить наверх относительно оси .
Для того чтобы построить график , нужно часть исходного графика, лежащую выше оси , оставить без изменения, а нижнюю отразить наверх относительно оси .
Пусть дан график 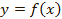 , построим график
, построим график 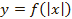 . Для начала раскроем модуль по определению:
. Для начала раскроем модуль по определению:
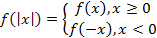
Следовательно, все точки с положительными или равными нулю абсциссами остаются без изменения, а все точки с отрицательными – заменяются точками с противоположными абсциссами (см. Рис. 19).
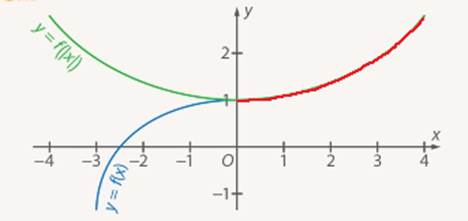
Рис. 19. Графики функций 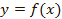 и
и 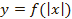 (красным цветом выделена общая часть этих графиков)
(красным цветом выделена общая часть этих графиков)
Для того чтобы построить график , нужно часть исходного графика, соответствующую значениям , оставить без изменений и отразить ее относительно оси для значений .
Задача 1
Построить график функции 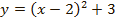 .
.
Решение
Построим график заданной функции последовательно (см. Рис. 20):
1. Строим график 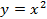 .
.
2. График 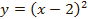 получается из графика
получается из графика 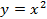 параллельным переносом последнего на 2 единицы вправо.
параллельным переносом последнего на 2 единицы вправо.
3. График 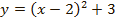 получается из графика функции
получается из графика функции 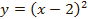 параллельным переносом последнего вдоль оси ординат на 3 единицы вверх.
параллельным переносом последнего вдоль оси ординат на 3 единицы вверх.
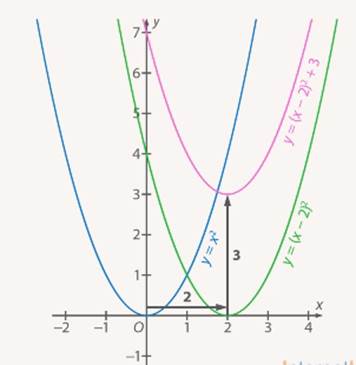
Рис. 20. Иллюстрация к задаче
Мы могли бы сделать операции в обратном порядке, то есть сначала поднять график 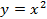 на 3 единицы вверх, а потом получившийся график сдвинуть вправо на 2 единицы (см. Рис. 21).
на 3 единицы вверх, а потом получившийся график сдвинуть вправо на 2 единицы (см. Рис. 21).
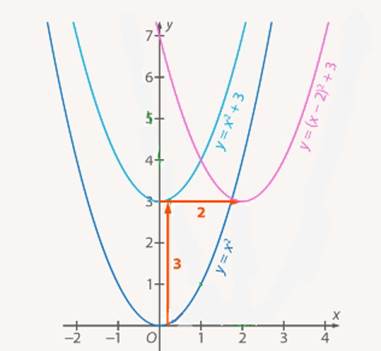
Рис. 21. Иллюстрация к задаче
Обратите внимание, что не все графики функций можно строить в произвольном порядке. Например, для построения графика 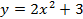 сначала нужно построить график
сначала нужно построить график 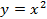 , затем график
, затем график 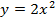 (растяжение от оси
(растяжение от оси 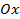 ), а далее – график
), а далее – график 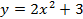 (параллельный перенос вдоль оси ординат) (см. Рис. 22). Если же сделать в другой последовательности, то есть построить
(параллельный перенос вдоль оси ординат) (см. Рис. 22). Если же сделать в другой последовательности, то есть построить 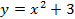 , то далее на 2 придется умножить всё выражение.
, то далее на 2 придется умножить всё выражение.
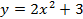
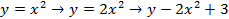 – ПРАВИЛЬНО
– ПРАВИЛЬНО
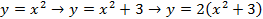 – НЕПРАВИЛЬНО
– НЕПРАВИЛЬНО
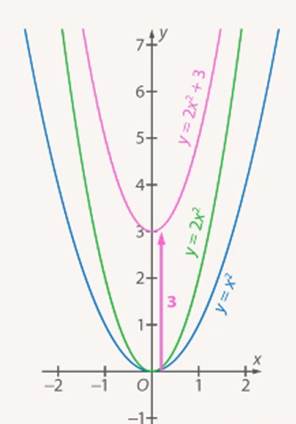
Рис. 22. Иллюстрация к задаче
Пример
Построить график 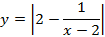 .
.
Решение
1. Строим график 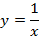 (гипербола) (см. Рис. 23).
(гипербола) (см. Рис. 23).
2. Строим график 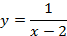 (из аргумента вычитается 2, следовательно, сдвигаем график
(из аргумента вычитается 2, следовательно, сдвигаем график 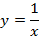 на 2 единицы вправо) (см. Рис. 23).
на 2 единицы вправо) (см. Рис. 23).
3. Строим график 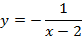 (домножение функции на (-1), следовательно, отражаем график
(домножение функции на (-1), следовательно, отражаем график 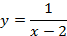 относительно оси
относительно оси 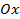 ) (см. Рис. 24).
) (см. Рис. 24).
4. Строим график 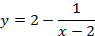 (добавление 2 к функции, следовательно, сдвигаем график
(добавление 2 к функции, следовательно, сдвигаем график 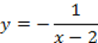 на 2 единицы вверх) (см. Рис. 24).
на 2 единицы вверх) (см. Рис. 24).
5. Строим график 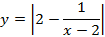 (модуль функции, следовательно, отражаем нижнюю часть графика
(модуль функции, следовательно, отражаем нижнюю часть графика 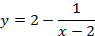 относительно оси
относительно оси 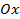 , а верхнюю оставляем без изменений) (см. Рис. 25).
, а верхнюю оставляем без изменений) (см. Рис. 25).
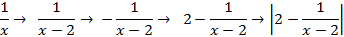
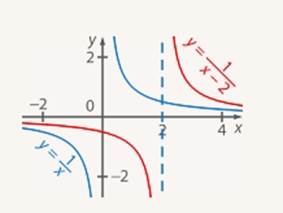
Рис. 23. Иллюстрация к задаче
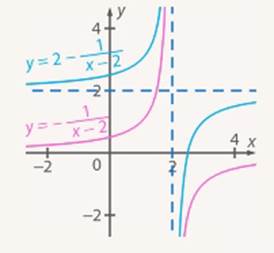
Рис. 24. Иллюстрация к задаче
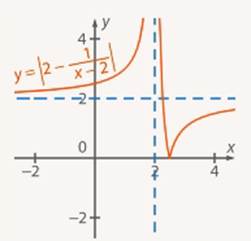
Рис. 25. Иллюстрация к задаче (искомый график)
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|