
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Минимизация расходов по перевозке туристов в гостиницы»
Решение.
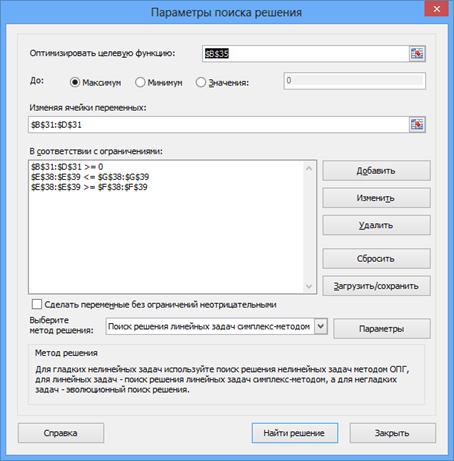
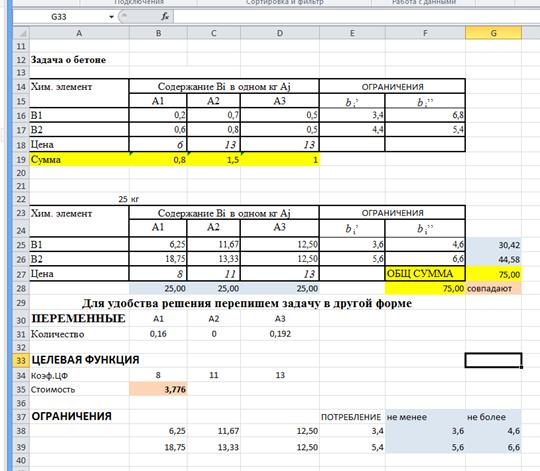
Вывод результаты моделирования в excel и Mathcad совпадают.
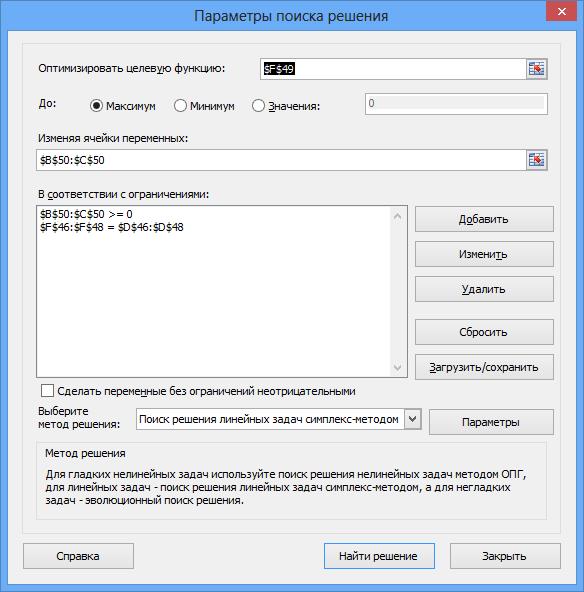
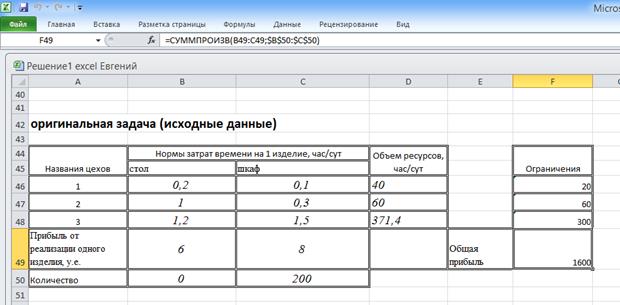
в) Оригинальная задача.
Вариант № 3.
Задача. Для производства столов и шкафов мебельная фабрика использует необходимые ресурсы. Нормы затрат ресурсов на одно изделие данного вида, прибыль от реализации одного изделия и общее количество имеющихся ресурсов каждого вида приведены в табл.
| Ресурсы | Нормы затрат ресурсов на одно изделие | Общее количество ресурсов | |
| стол | шкаф | ||
| Древесина (м3): | |||
| 1 вида | 0,2 | 0,1 | |
| 2 вида | 0,1 | 0,3 | |
| Трудоемкость (человеко-час) | 1,2 | 1,5 | 371,4 |
| Прибыль от реализации одного изделия (руб) | |||
Определить, сколько столов и шкафов следует изготовлять, чтобы прибыль от их реализации была максимальной.
Решение.
Предположим, что будет изготовлено 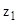 единиц столов,
единиц столов, 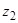 единиц шкофов. Тогда для производства такого количества изделий потребуется затратить древесины 1 вида 0,2z1+0,1z2 м3. Общий количество древесины 1 вида не может превышать 40, то должно выполняться неравенство 0,2z1+0,1z2£40.
единиц шкофов. Тогда для производства такого количества изделий потребуется затратить древесины 1 вида 0,2z1+0,1z2 м3. Общий количество древесины 1 вида не может превышать 40, то должно выполняться неравенство 0,2z1+0,1z2£40.
Рассуждая аналогично получим ограничения по остальным ресурсам:
древесины 2 вида: 0,1z1+0,3z2£60,
трудоемкость.: 1,2z1+1,5z2£371,4,
При этом, количество изготавливаемых изделий не может быть отрицательным: 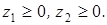 Прибыль от реализации изделий составит
Прибыль от реализации изделий составит 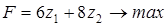 .
.
2) Транспортная задача (ТЗ):
а) Типовое задание №1: «Минимизация расходов на доставку продукции заказчикам со складов фирмы»;
Необходимо решить транспортную задачу: минимизировать расходы на доставку продукции заказчикам со складов фирмы, учитывая следующие затраты на доставку одной единицы продукции, объём заказа и количество продукции, хранящейся на каждом складе. Тарифы на перевозку единицы продукции, объёмы запасов продукции на складах, а также объёмы заказанной продукции представлены в таблице
Вариант № 13.
| Склад | Магазины заказчика | Запасы на складе (ед. прод) | ||||
| “Канц. товары | “Школьник” | “Детский мир” | “Учебные принадлежности” | Фиктивный потребитель | ||
| Смоленская | 1,5 | 0,5 | ||||
| Митино | 0,5 | 2,5 | ||||
| Перово | ||||||
| Калужская | 0,5 | 1,5 | ||||
| Объём заказа | ||||||
Для всех вариантов необходимо записать математическую формулировку транспортной задачи и решить ее в двух вариантах:
Решение.
В данной транспортной задаче не выполняется равенство: сумма запасов не равна сумме объемов заказа, следовательно, имеем задачу с неправильным балансом, а модель задачи является открытой. Объем заказа(10+20+30+15=75), Запасы (25+20+30+10=85).
Приведем открытую транспортную задачу к сбалансированнойТ.к. имеем превышение запасов над потребностями. В этом случае вводится “фиктивный” потребитель с потребностями равными абсолютной величине разности между общим количеством запасов и общим количеством требуемых единиц. Стоимость по доставке будет для этого фиктивного потребителя равна 0, т.к. поставки фактически нет.
Далее решаем поставленную задачу как уже классическую.
Переменными (неизвестными) транспортной задачи являются xij , i=1,2,...,m j=1,2,...,n — объемы перевозок от i-го поставщика каждому j-му потребителю. Эти переменные могут быть записаны в виде матрицы перевозок:
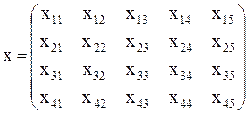
Так как произведение Cij*xij определяет затраты на перевозку груза от i-го поставщика j-му потребителю, то суммарные затраты на перевозку всех грузов равны: 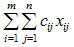 .
.
По условию задачи требуется обеспечить минимум суммарных затрат. Следовательно, целевая функция задачи имеет вид:
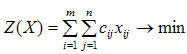
Система ограничений задачи состоит из двух групп уравнений. Первая группа уравнений описывает тот факт, что запасы всех поставщиков вывозятся полностью и имеет вид:
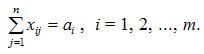
Вторая группа уравнений выражает требование удовлетворить запросы всех потребителей полностью и имеет вид:
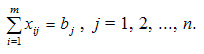
Необходимо учесть условие неотрицательности объемов перевозок.
Таким образом, математическая постановка задачи записывается в следующем виде
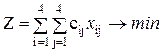 ,
,
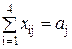 ,
,
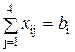 ,
,
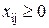 .
.
б) Типовое задание №2: «Минимизация расходов по перевозке туристов в гостиницы»;
Типовое задание №2
«Минимизация расходов по перевозке туристов в гостиницы»
Задание: Туристической фирме необходимо разместить три группы туристов Т1, Т2, Т3 количеством 60 + k, 120 + k и 100 + k человек соответственно, прибывших в аэропорты, по четырем гостиницам Г1, Г2, Г3, Г4. Стоимость перевозки одного туриста и количество свободных номеров в гостиницах указаны в таблице 4.2.
Таблица 4.2. Числовые данные для типового задания №2
|
Группы | Количество туристов | Стоимость перевозки одного туриста из аэропорта в гостиницу | |||
| Г1 | Г2 | Г3 | Г4 | ||
| Т1 | 60 + k | ||||
| Т2 | 120 + k | ||||
| Т3 | 100 + k | ||||
| Количество свободных мест в гостинице | 20+ k | 110 + k | 40+ k | ||
Составить план перевозок туристов из аэропортов в гостиницы, который обеспечит минимальные транспортные издержки при условиях размещения всех туристов и заполнения всех свободных мест в гостиницах.
Примечание: k–номер варианта.k=13
Решение:
В данной транспортной задаче выполняется равенство: сумма количества свободных мест и общее количество пассажиров, следовательно, имеем задачу закрытую.
Переменными (неизвестными) транспортной задачи являются xij , i=1,2,...,m j=1,2,...,n — количество доставленных в гостиницу пассажиров от i-ой группы в j-ю гостиницу. Эти переменные могут быть записаны в виде матрицы перевозок:
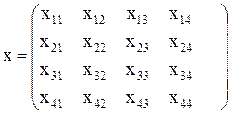
Так как произведение Cij*xij определяет затраты на перевозку пассажиров, то суммарные затраты на перевозку всех:
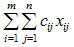 .
.
По условию задачи требуется обеспечить минимум суммарных затрат. Следовательно, целевая функция задачи имеет вид:
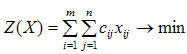
Система ограничений задачи состоит из двух групп уравнений. Уравнений описывает тот факт, что должны быть размещены все пассажиры в имеющихся местах в гостиницах:
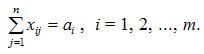
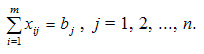
Необходимо учесть условие неотрицательности объемов перевозок.
Таким образом, математическая постановка задачи записывается в следующем виде
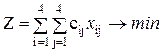 ,
,  ,
, 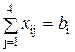 ,
, 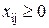 .
.
в) Оригинальная (индивидуальная) задача.
¨Исходные данные задач для каждого варианта приведены в Приложении Б4.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|