- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Таблица 1.1. Кодирование источника по методу Шеннона-Фано
Таблица 1.1. Кодирование источника по методу Шеннона-Фано
|
|
| Выбор символов неравномерного кода |
| |||
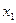
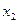
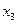
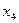
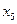

| 0,4 0,3 0,1 0,08 0,07 0,05 | |||||
На 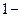 ом этапе множество символов делим на
ом этапе множество символов делим на 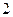 части:
части: 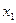 и
и 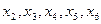 ; на
; на 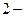 ом -
ом - 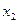 и
и 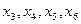 ; на
; на 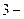 ем -
ем - 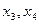 и
и 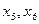 ; на
; на  ом -
ом - 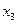 и
и 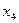 ,
, 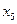 и
и  . Более вероятным символам источника присвоим кодовые слова меньшей длины
. Более вероятным символам источника присвоим кодовые слова меньшей длины 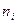 . Построили префиксный код. Средняя длина кодового слова (среднее число символов кода на один символ источника)
. Построили префиксный код. Средняя длина кодового слова (среднее число символов кода на один символ источника) 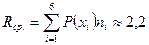 .
.
Помехоустойчивые коды бывают блоковые и непрерывные. При блоковом кодировании последовательность символов источника разбивают на отрезки. Каждому отрезку соответствует определенная последовательность (блок) кодовых символов - кодовое слово. Множество кодовых слов, возможных при данном способе кодирования, образует блоковый код. В равномерном (неравномерном) коде длина блока - постоянная (переменная). Помехоустойчивые коды - обычно равномерные.
Блоковые коды бывают разделимые и неразделимые. В разделимом коде  длины
длины 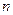 символы можно разделить по назначению на
символы можно разделить по назначению на 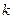 информационных (несущих информацию о сообщении) и
информационных (несущих информацию о сообщении) и 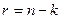 проверочных. Скорость кода
проверочных. Скорость кода 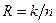 . Полное число слов в коде равно
. Полное число слов в коде равно 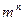 , а
, а 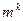 - число разрешенных слов. В неразделимых кодах нельзя выделить информационные и проверочные символы. Например, - это коды с постоянным весом и коды на основе матриц Адамара (см. п. 6.3). В двоичном коде с постоянным весом кодовые слова содержат одинаковое число
- число разрешенных слов. В неразделимых кодах нельзя выделить информационные и проверочные символы. Например, - это коды с постоянным весом и коды на основе матриц Адамара (см. п. 6.3). В двоичном коде с постоянным весом кодовые слова содержат одинаковое число 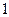 . В стандартном телеграфном коде № 3 любое из них содержит три
. В стандартном телеграфном коде № 3 любое из них содержит три 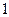 и четыре
и четыре 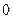
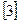 .
.
Разделимые коды бывают линейные и нелинейные. В линейных кодах сумма по 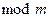 (см. (1.1))
(см. (1.1)) 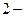 х любых кодовых слов образует кодовое слово того же кода. Линейный код называется систематическим, если первые
х любых кодовых слов образует кодовое слово того же кода. Линейный код называется систематическим, если первые 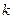 символов любого его кодового слова являются информационными, а остальные
символов любого его кодового слова являются информационными, а остальные 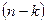 - проверочными. Подкласс линейных кодов - циклические коды (см. п. 6.5). В них все наборы, образованные циклической перестановкой символов в любом кодовом слове, являются кодовыми словами того же кода. Это свойство упрощает построение кодека, особенно – при обнаружении и исправлении одиночных ошибок. Примеры циклических кодов - коды Хэмминга, коды Боуза-Чоудхури-Хоквингема (БЧХ-коды) и другие. Пример нелинейного двоичного кода - код Бергера (см. п. 1.4). В нем проверочные символы образованы двоичной записью числа
- проверочными. Подкласс линейных кодов - циклические коды (см. п. 6.5). В них все наборы, образованные циклической перестановкой символов в любом кодовом слове, являются кодовыми словами того же кода. Это свойство упрощает построение кодека, особенно – при обнаружении и исправлении одиночных ошибок. Примеры циклических кодов - коды Хэмминга, коды Боуза-Чоудхури-Хоквингема (БЧХ-коды) и другие. Пример нелинейного двоичного кода - код Бергера (см. п. 1.4). В нем проверочные символы образованы двоичной записью числа 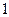 в последовательности информационных символов.
в последовательности информационных символов.
Непрерывное кодирование и декодирование делают над непрерывной последовательностью символов без разбиения ее на блоки. Среди непрерывных наиболее часто применяют сверточные коды (см. п. 6.8).
Различают каналы связи с независимыми и группирующимися ошибками. Соответственно, помехоустойчивые коды можно разбить на 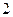 класса: исправляющие независимые ошибки и исправляющие пакеты ошибок. Для исправления последних есть много эффективных кодов. На практике целесообразнее применять коды, исправляющие независимые ошибки, вместе с устройством перемежения символов (декорреляции ошибок). Тогда символы кодового слова не передаются последовательно, а перемешиваются с символами других кодовых слов. Если интервал между символами каждого кодового слова сделать больше ²памяти² канала, ошибки в пределах одного слова станут независимыми. Это и позволяет применять коды, исправляющие независимые ошибки.
класса: исправляющие независимые ошибки и исправляющие пакеты ошибок. Для исправления последних есть много эффективных кодов. На практике целесообразнее применять коды, исправляющие независимые ошибки, вместе с устройством перемежения символов (декорреляции ошибок). Тогда символы кодового слова не передаются последовательно, а перемешиваются с символами других кодовых слов. Если интервал между символами каждого кодового слова сделать больше ²памяти² канала, ошибки в пределах одного слова станут независимыми. Это и позволяет применять коды, исправляющие независимые ошибки.
В Приложении проиллюстрированы принципы построения кодов и сжатия данных на примере компьютерных сетей.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|