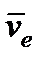Теорема. При поступательном движении все точки тела описывают совпадающие при наложении траектории и имеют в данный момент времени одинаковые скорости и ускорения.
Теорема. При поступательном движении все точки тела описывают совпадающие при наложении траектории и имеют в данный момент времени одинаковые скорости и ускорения.
Пусть тело (рис.9), двигаясь поступательно, переместилось из положения АВ в положение А'В'. Фигура АВА'В' - параллелограмм, т.к. стороны АВ и А'В' равны и параллельны. Следовательно, перемещения точек А и В также будут равны и параллельны, т.е. Δ 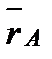 = Δ = Δ 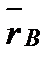 . Из рисунка видно, что траектория т. В получается из траектории т. А смещением на . Из рисунка видно, что траектория т. В получается из траектории т. А смещением на 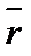 , т.е. траектории совпадают при наложении. Взяв два раза производную от равенства , т.е. траектории совпадают при наложении. Взяв два раза производную от равенства 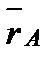 = = 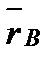 , получим: , получим: 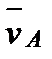 = = 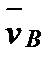 ; ; 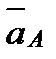 = = 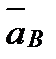 . Что и требовалось доказать. . Что и требовалось доказать.
Тоесть при изучении поступательного движения тела достаточно изучить движение хотя бы одной его точки, а для этого можно использовать теорию, полученную в кинематике точки.
| 12. Вращательное движение. Угловые скорость и ускорение
Вращательным называется такое движение твердого тела, при котором имеются две точки, остающиеся все время неподвижными.
Линия, проходящая через эти две точки, называется осью вращения. Все точки, лежащие на оси вращения, неподвижны. Положение вращающегося тела можно задать с помощью двугранного угла φ (рис.10) между неподвижной полуплоскостью (н.п.) и подвижной полуплоскостью (п.п.), жестко связанной с телом. Угол φ положителен, если для наблюдателя, смотрящего с положительного конца оси вращения, поворот виден происходящим против часовой стрелки. Для задания вращения надо задать функцию, описывающую изменение угла φ во времени: φ=φ(t). Это и есть закон вращательного движения. Основными кинематическими характеристиками вращательного движения являются угловая скорость ω (рад/с; 1/с) и угловое ускорение ε (рад/с 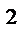 ; 1/с2). Эти величины вводятся по аналогии с понятиями скорости и ускорения точки.Угловая скорость ω (омега) есть предел, к которому стремится отношение приращения угла поворота Δφ к промежутку времени ; 1/с2). Эти величины вводятся по аналогии с понятиями скорости и ускорения точки.Угловая скорость ω (омега) есть предел, к которому стремится отношение приращения угла поворота Δφ к промежутку времени  Δt, за которое это приращение произошло, при стремлении Δt к нулю. Угловое ускорение ε (ипсилон) есть предел отношения приращения угловой скорости к промежутку времени, при стремлении последнего к нулю. Очевидно, эти пределы равны первым производным от угла и угловой скорости по времени, то есть Δt, за которое это приращение произошло, при стремлении Δt к нулю. Угловое ускорение ε (ипсилон) есть предел отношения приращения угловой скорости к промежутку времени, при стремлении последнего к нулю. Очевидно, эти пределы равны первым производным от угла и угловой скорости по времени, то есть
ω = dφ/dt; ε = dω /dt = d2φ/dt2.
В технике часто угловая скорость задается в об/мин. В этом случае она называется частотой вращения и обозначается буквой n. Связь между ω и n имеет вид
ω =π×n /30 .
Движение тела называется плоским, если все точки тела перемещаются в плоскостях, параллельных некоторой неподвижной плоскости.
Очевидно, что точки, лежащие на перпендикуляре А1А2 к сечению S, параллельному неподвижной плоскости, двигаются так же, как т. А. Следовательно, для изучения движения всего тела достаточно изучить движение сечения S. Положение сечения S определяется положением отрезка АВ (рис.13). Для задания положения отрезка АВ достаточно задать координаты х и у т. А, а также угол φ между АВ и осью x. Для задания движения сечения S надо задать три функции определяющие х, у и φ в каждый момент времени. Таким образом, уравнения плоского движения имеют вид
Зная эти уравнения, можно написать уравнение движения любой точки тела. Если φ = соnst, то тело будет совершать поступательное движение. следовательно, первые два уравнения его и описывают. Если xA и yA= соnst, то тело будет совершать вращательное движение. следовательно, его описывает последнее уравнение. Плоское движение можно представить как сумму двух движений: поступательного − вместе с полюсом А и вращательного − вокруг точки А.
|

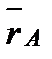 = Δ
= Δ 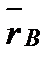 . Из рисунка видно, что траектория т. В получается из траектории т. А смещением на
. Из рисунка видно, что траектория т. В получается из траектории т. А смещением на 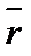 , т.е. траектории совпадают при наложении. Взяв два раза производную от равенства
, т.е. траектории совпадают при наложении. Взяв два раза производную от равенства 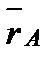 =
= 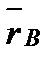 , получим:
, получим: 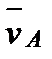 =
= 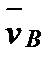 ;
; 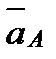 =
= 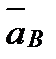 . Что и требовалось доказать.
. Что и требовалось доказать.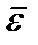
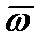
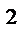 ; 1/с2). Эти величины вводятся по аналогии с понятиями скорости и ускорения точки.Угловая скорость ω (омега) есть предел, к которому стремится отношение приращения угла поворота Δφ к промежутку времени
; 1/с2). Эти величины вводятся по аналогии с понятиями скорости и ускорения точки.Угловая скорость ω (омега) есть предел, к которому стремится отношение приращения угла поворота Δφ к промежутку времени  Δt, за которое это приращение произошло, при стремлении Δt к нулю. Угловое ускорение ε (ипсилон) есть предел отношения приращения угловой скорости к промежутку времени, при стремлении последнего к нулю. Очевидно, эти пределы равны первым производным от угла и угловой скорости по времени, то есть
Δt, за которое это приращение произошло, при стремлении Δt к нулю. Угловое ускорение ε (ипсилон) есть предел отношения приращения угловой скорости к промежутку времени, при стремлении последнего к нулю. Очевидно, эти пределы равны первым производным от угла и угловой скорости по времени, то есть
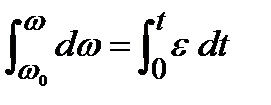 , получим закон изменения угловой скорости при равнопеременном движении:
ω – ω0 = εt, или ω = ω0 + εt. (14.1)
Учитывая, что ω = dφ/dt , разделяя переменные и интегрируя еще один раз, получим закон равнопеременного вращения: φ = φ0+ ω0 t+1/2 εt
, получим закон изменения угловой скорости при равнопеременном движении:
ω – ω0 = εt, или ω = ω0 + εt. (14.1)
Учитывая, что ω = dφ/dt , разделяя переменные и интегрируя еще один раз, получим закон равнопеременного вращения: φ = φ0+ ω0 t+1/2 εt 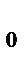 + ω
+ ω 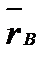
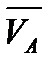
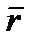
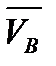


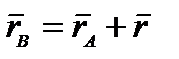 . Возьмем производную. Из кинематики точки известно, что d
. Возьмем производную. Из кинематики точки известно, что d 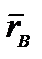 /dt =
/dt = 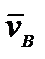 ; d
; d 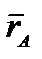 /dt =
/dt = 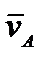 . Обозначим d
. Обозначим d 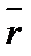 /dt =
/dt = 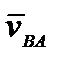 , тогда получим
, тогда получим 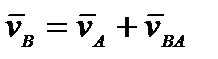 − это и есть теорема о сложении скоростей при плоском движении. Очевидно,
− это и есть теорема о сложении скоростей при плоском движении. Очевидно, 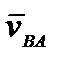 − это скорость движения т. В, когда т. А неподвижна, т. е. когда тело вращается вокруг полюса А.
− это скорость движения т. В, когда т. А неподвижна, т. е. когда тело вращается вокруг полюса А. 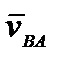 − это скорость вращения т. В вокруг полюса А. Тогда
− это скорость вращения т. В вокруг полюса А. Тогда 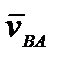 | АВ. По формуле Эйлера
| АВ. По формуле Эйлера 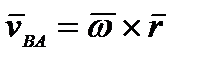 , тогда теорема примет вид
, тогда теорема примет вид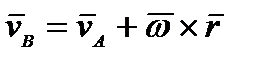
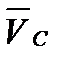
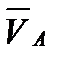
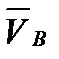
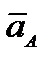
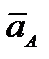
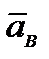
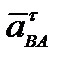
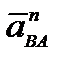
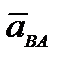
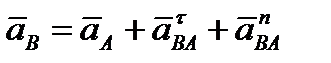 .
.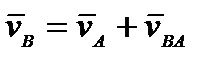 . Возьмем производную. тогда, поскольку d
. Возьмем производную. тогда, поскольку d 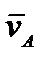 /dt =
/dt = 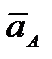 , a d
, a d 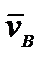 /dt =
/dt = 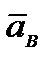 , то
, то 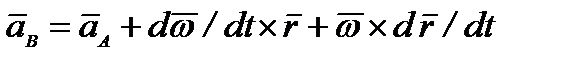 ; но
; но 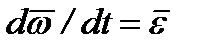 , а d
, а d  /dt =
/dt = 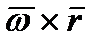 , тогда
, тогда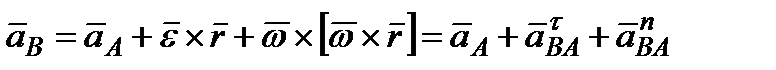 .
.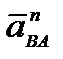 − вектор нормального (центростремительного) ускорения при вращении т. В вокруг т. А. Он направлен от т. В к т. А (рис.20),
− вектор нормального (центростремительного) ускорения при вращении т. В вокруг т. А. Он направлен от т. В к т. А (рис.20), 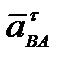 − вектор тангенциального (касательного) ускорения при вращении т. В вокруг т. А. Он направлен перпендикулярно АВ в сторону углового ускорения
− вектор тангенциального (касательного) ускорения при вращении т. В вокруг т. А. Он направлен перпендикулярно АВ в сторону углового ускорения 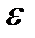 . По величине
. По величине  = ω
= ω 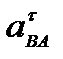 = ε ∙AB.
= ε ∙AB.