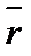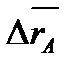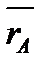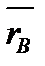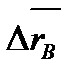Ускорение при координатном способе задания движения
Векторный способ задания движения точки.Задать движение − это значит уметь определить положение точки в каждый момент времени. Векторный способ задания движения заключается в задании вектор функции: 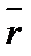 = = 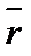 (t). Подставляя в нее значения времени t (t). Подставляя в нее значения времени t  ; t ; t 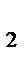 ; ... , получим векторы ; ... , получим векторы 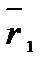 = = 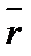 (t (t 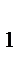 ), ), 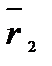 = = 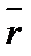 (t (t 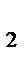 ), .. , которые определяют положение точки в эти моменты времени (рис.1). Построить вектор можно только в некоторой системе координат. Векторный способ подразумевает наличие системы координат, но не конкретизирует ее, поэтому им пользуются при выводе теоретических положений.
Линия, которую описывает точка при своем движении, называется траекторией. ), .. , которые определяют положение точки в эти моменты времени (рис.1). Построить вектор можно только в некоторой системе координат. Векторный способ подразумевает наличие системы координат, но не конкретизирует ее, поэтому им пользуются при выводе теоретических положений.
Линия, которую описывает точка при своем движении, называется траекторией.
| 2. Координатный способ задания движения точки.При этом способе задается три функции (при движении в пространстве), определяющие три координаты точки в каждый момент времени. Системы координат могут быть разными, например: прямоугольная декартова, цилиндрическая или сферическая система координат. В первом случае задается: х=х(t); y=у(t); z=z(t) − это и есть уравнения движения точки (рис.2). в цилиндрической системе координат (рис.3) задаются: ρ= ρ(t); φ= φ (t); z=z(t). В сферической (рис.4): φ = φ(t); θ= θ(t); r=r(t). если движение задано в какой - то из этих систем координат, то всегда можно перейти к заданию движения в любой из двух других
| 3. Естественный способ задания движения точки
Он заключается в задании (рис.5):
1) траектории точки: у = f(х);
2) начала отсчета (т. О);
3) положительного направления отсчета;
4) закона движения s = s(t), где s − дуговая
координата.
| 4. Естественные оси координат
Естественные оси двигаются вместе с точкой и изменяют свое положение в пространстве. Этих осей три (рис.6): касательная, главная нормаль, бинормаль.Единичный вектор касательной − 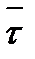 (тау) направлен по касательной к траектории в сторону положительного отсчета дуги.Соприкасающаяся плоскость − предельное положение плоскости, проходящей через т. М1, лежащую на кривой, и касательную в т. М, при стремлении т. М1 к т. М. Единичный вектор главной нормали (тау) направлен по касательной к траектории в сторону положительного отсчета дуги.Соприкасающаяся плоскость − предельное положение плоскости, проходящей через т. М1, лежащую на кривой, и касательную в т. М, при стремлении т. М1 к т. М. Единичный вектор главной нормали 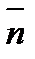 перпендикулярен перпендикулярен 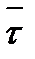 , лежит в соприкасающейся плоскости и направлен в сторону вогнутости траектории. Плоскость перпендикулярная касательной называется нормальной. Единичный вектор бинормали , лежит в соприкасающейся плоскости и направлен в сторону вогнутости траектории. Плоскость перпендикулярная касательной называется нормальной. Единичный вектор бинормали 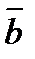 перпендикулярен соприкасающейся плоскости . перпендикулярен соприкасающейся плоскости .
| 9. Скорость при естественном способе задании движения
Известно : 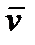 = lim Δ = lim Δ 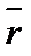 /Δt = lim Δ /Δt = lim Δ 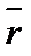 /Δs ∙ limΔs/ Δt.
Δt /Δs ∙ limΔs/ Δt.
Δt 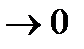 Δs Δs 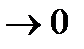 Δt Δt 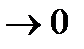 Так как первый предел по модулю равен единице, а направлен по касательной, то он равен
Так как первый предел по модулю равен единице, а направлен по касательной, то он равен 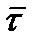 (тау); обозначим: ds/dt = v τ , тогда (тау); обозначим: ds/dt = v τ , тогда 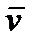 = v τ∙ = v τ∙  . .
| 10. Ускорение при естественном способе задания движения.Известно, что 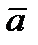 = d = d  / dt = d v τ / dt ∙ / dt = d v τ / dt ∙  + v τ ∙ d + v τ ∙ d  /dt. Можно показать, что d /dt. Можно показать, что d  /dt = v τ /ρ ∙ /dt = v τ /ρ ∙ 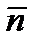 . Тогда формула примет вид . Тогда формула примет вид
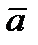 = d v τ / dt ∙ = d v τ / dt ∙  + v + v 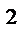 τ / ρ ∙ τ / ρ ∙ 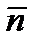 (10.1') с другой стороны, (10.1') с другой стороны, 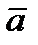 = a τ ∙ = a τ ∙  + an ∙ + an ∙ 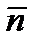 + аb ∙ + аb ∙ 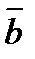 . (10.2) сравнивая (10.1') и (10.2), получим
a τ = d v τ / dt; an = v . (10.2) сравнивая (10.1') и (10.2), получим
a τ = d v τ / dt; an = v 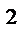 τ / ρ; аb = 0.
здесь ρ - радиус кривизны траектории, величина обратная кривизне k: ρ = 1/ k.
По определению k = lim ε / Δs, где ε - угол смежности (угол между касатель
ными в двух точках кривой, лежащих на расстоянии Δs). Радиус кривизны − это радиус максимальной окружности, которую можно вписать в кривую в данной точке. Радиус кривизны окружности равен радиусу окружности, у прямой он равен ∞. τ / ρ; аb = 0.
здесь ρ - радиус кривизны траектории, величина обратная кривизне k: ρ = 1/ k.
По определению k = lim ε / Δs, где ε - угол смежности (угол между касатель
ными в двух точках кривой, лежащих на расстоянии Δs). Радиус кривизны − это радиус максимальной окружности, которую можно вписать в кривую в данной точке. Радиус кривизны окружности равен радиусу окружности, у прямой он равен ∞.
| | 5. Скорость при векторном способе задания движения
Пусть за время Δt точка переместилась из М в М  (рис.7) , вектор Δ (рис.7) , вектор Δ 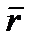 − вектор перемещения. Средней скоростью точки за время Δt называется вектор − вектор перемещения. Средней скоростью точки за время Δt называется вектор  ср = Δ ср = Δ 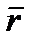 /Δt. Скоростью точки в данный момент времени называется предел, к которому стремится отношение вектора перемещения к промежутку времени, за которое оно произошло, при стремлении последнего к нулю : /Δt. Скоростью точки в данный момент времени называется предел, к которому стремится отношение вектора перемещения к промежутку времени, за которое оно произошло, при стремлении последнего к нулю :
 = lim Δ = lim Δ 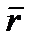 /Δt . /Δt .
Δt 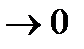
Из рис. 7 видно, что 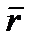 (t) + Δ (t) + Δ 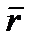 = = 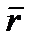 (t+Δt), (t+Δt),
тогда Δ 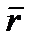 = = 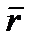 (t+Δt) - (t+Δt) - 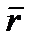 (t), и (t), и
 = lim Δ = lim Δ 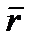 /Δt = lim( /Δt = lim( 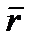 (t+Δt) - (t+Δt) - 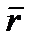 (t)) / Δt = d (t)) / Δt = d 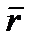 / dt. / dt.
Δt  Δt Δt 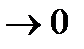
то есть скорость точки в данный момент времени равна первой производной от радиуса вектора по времени. Поскольку вектор Δ 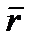 в пределе занимает положение касательной, то и вектор скорости в данный момент времени направлен по касательной к траектории. Скорость измеряется в м/с. в пределе занимает положение касательной, то и вектор скорости в данный момент времени направлен по касательной к траектории. Скорость измеряется в м/с.
| 6. Ускорение при векторном способе задания движения
Средним ускорением называется отношение вектора изменения скорости к промежутку времени, за которое оно произошло: 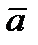 ср=Δ ср=Δ  /Δt. /Δt.
Ускорением точки в данный момент называется предел этого отношения при стремлении промежутка времени к нулю.
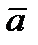 = lim Δ = lim Δ  /Δt = lim( /Δt = lim(  (t+ Δt) - (t+ Δt) -  (t))/ Δt. (t))/ Δt.
Δt 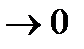 Δt Δt 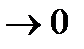
Ускорение равно первой производной от скорости, или второй производной от радиуса вектора по времени:
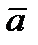 = d = d  /dt = d /dt = d 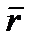 /dt /dt 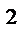 . .
Ускорение 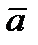 ср, а значит и ускорение в данный момент времени ср, а значит и ускорение в данный момент времени 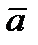 , направлено в сторону вогнутости траектории (рис.8). Ускорение измеряется в м/с2. , направлено в сторону вогнутости траектории (рис.8). Ускорение измеряется в м/с2.
| | Скорость при координатном способе задания движения
Известно, что  =d =d 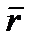 /dt, но /dt, но 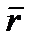 =x· =x· 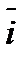 +y· +y· 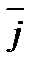 +z· +z· 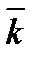 , тогда (т.к. , тогда (т.к. 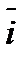 , , 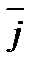 , , 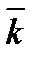 - const) - const)
 = dx/dt· = dx/dt· 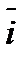 +dy/dt· +dy/dt· 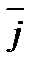 +dz/dt· +dz/dt· 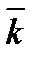 .
С другой стороны, .
С другой стороны,  = v = v 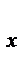 · · 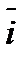 +v +v 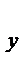 · · 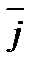 +v +v 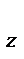 · · 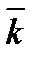 . сравнивая (1) и (2) получим: vх = dx/dt; vу = dy/dt; v . сравнивая (1) и (2) получим: vх = dx/dt; vу = dy/dt; v 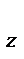 = dz/dt.
то есть: проекция скорости на ось равна первой производной от соответствующей координаты по времени. Зная проекции, можно найти модуль скорости: = dz/dt.
то есть: проекция скорости на ось равна первой производной от соответствующей координаты по времени. Зная проекции, можно найти модуль скорости:
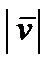 = = 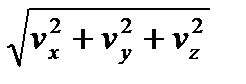 ,
а также направляющие косинусы:
соs( ,
а также направляющие косинусы:
соs(  ; ; 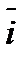 ) = vx / | ) = vx / |  | ; соs( | ; соs(  ; ; 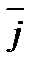 ) = vy / | ) = vy / |  |; соs( |; соs(  ; ; 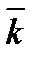 ) = vz / | ) = vz / |  |. |.
| |
8. Ускорение при координатном способе задания движения
Известно, что 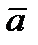 = d = d  /dt, но /dt, но  = vx· = vx· 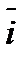 + vy· + vy· 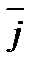 + vz· + vz· 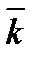 , тогда , тогда
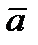 = dv x /d t · = dv x /d t · 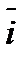 +dvy /d t · +dvy /d t · 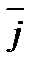 +dvz /dz · +dvz /dz · 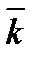 , (8.1) , (8.1)
с другой стороны, 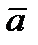 = ах · = ах · 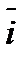 + ау · + ау · 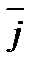 + аz· + аz· 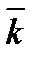 . (8.2) . (8.2)
сравнивая (8.1) и (8.2), получим:
а x =dv x /dt =d 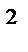 x / dt x / dt 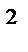 ; аy=dvy/ dt =d ; аy=dvy/ dt =d 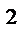 y / dt y / dt 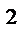 ; а ; а 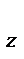 =dvz /dt =d =dvz /dt =d 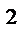 z / dt z / dt 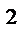 . .
то есть: проекция ускорения на ось равна первой производной от проекции скорости на ту же ось, или второй производной от соответствующей координаты по времени.
Модуль ускорения | 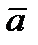 | = | = 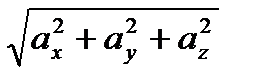 ; направляющие косинусы: ; направляющие косинусы:
соs ( 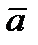 ; ; 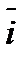 ) = аx / | ) = аx / | 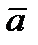 |; соs( |; соs( 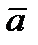 ; ; 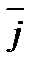 ) = аy / | ) = аy / | 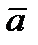 |; соs ( |; соs ( 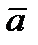 ; ; 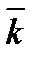 ) = аz / | ) = аz / | 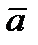 |. |.
|
| 11. Поступательное движение твердого тела
Поступательным называется такое движение тела, при котором любая прямая, жестко соединенная с ним, остается параллельной своему начальному положению. |
|

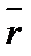 =
= 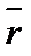 (t). Подставляя в нее значения времени t
(t). Подставляя в нее значения времени t 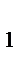 ; t
; t 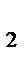 ; ... , получим векторы
; ... , получим векторы 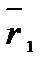 =
= 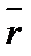 (t
(t 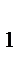 ),
), 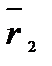 =
= 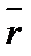 (t
(t 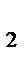 ), .. , которые определяют положение точки в эти моменты времени (рис.1). Построить вектор можно только в некоторой системе координат. Векторный способ подразумевает наличие системы координат, но не конкретизирует ее, поэтому им пользуются при выводе теоретических положений.
Линия, которую описывает точка при своем движении, называется траекторией.
), .. , которые определяют положение точки в эти моменты времени (рис.1). Построить вектор можно только в некоторой системе координат. Векторный способ подразумевает наличие системы координат, но не конкретизирует ее, поэтому им пользуются при выводе теоретических положений.
Линия, которую описывает точка при своем движении, называется траекторией.
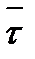 (тау) направлен по касательной к траектории в сторону положительного отсчета дуги.Соприкасающаяся плоскость − предельное положение плоскости, проходящей через т. М1, лежащую на кривой, и касательную в т. М, при стремлении т. М1 к т. М. Единичный вектор главной нормали
(тау) направлен по касательной к траектории в сторону положительного отсчета дуги.Соприкасающаяся плоскость − предельное положение плоскости, проходящей через т. М1, лежащую на кривой, и касательную в т. М, при стремлении т. М1 к т. М. Единичный вектор главной нормали 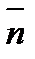 перпендикулярен
перпендикулярен 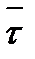 , лежит в соприкасающейся плоскости и направлен в сторону вогнутости траектории. Плоскость перпендикулярная касательной называется нормальной. Единичный вектор бинормали
, лежит в соприкасающейся плоскости и направлен в сторону вогнутости траектории. Плоскость перпендикулярная касательной называется нормальной. Единичный вектор бинормали 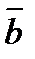 перпендикулярен соприкасающейся плоскости .
перпендикулярен соприкасающейся плоскости .
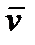 = lim Δ
= lim Δ 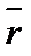 /Δt = lim Δ
/Δt = lim Δ 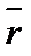 /Δs ∙ limΔs/ Δt.
Δt
/Δs ∙ limΔs/ Δt.
Δt 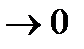 Δs
Δs 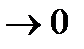 Δt
Δt 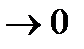 Так как первый предел по модулю равен единице, а направлен по касательной, то он равен
Так как первый предел по модулю равен единице, а направлен по касательной, то он равен 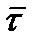 (тау); обозначим: ds/dt = v τ , тогда
(тау); обозначим: ds/dt = v τ , тогда 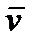 = v τ∙
= v τ∙  .
.
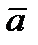 = d
= d  / dt = d v τ / dt ∙
/ dt = d v τ / dt ∙  + v τ ∙ d
+ v τ ∙ d  /dt. Можно показать, что d
/dt. Можно показать, что d  /dt = v τ /ρ ∙
/dt = v τ /ρ ∙ 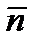 . Тогда формула примет вид
. Тогда формула примет вид
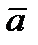 = d v τ / dt ∙
= d v τ / dt ∙  + v
+ v 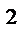 τ / ρ ∙
τ / ρ ∙ 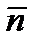 (10.1') с другой стороны,
(10.1') с другой стороны, 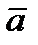 = a τ ∙
= a τ ∙  + an ∙
+ an ∙ 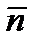 + аb ∙
+ аb ∙ 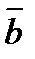 . (10.2) сравнивая (10.1') и (10.2), получим
a τ = d v τ / dt; an = v
. (10.2) сравнивая (10.1') и (10.2), получим
a τ = d v τ / dt; an = v 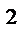 τ / ρ; аb = 0.
здесь ρ - радиус кривизны траектории, величина обратная кривизне k: ρ = 1/ k.
По определению k = lim ε / Δs, где ε - угол смежности (угол между касатель
ными в двух точках кривой, лежащих на расстоянии Δs). Радиус кривизны − это радиус максимальной окружности, которую можно вписать в кривую в данной точке. Радиус кривизны окружности равен радиусу окружности, у прямой он равен ∞.
τ / ρ; аb = 0.
здесь ρ - радиус кривизны траектории, величина обратная кривизне k: ρ = 1/ k.
По определению k = lim ε / Δs, где ε - угол смежности (угол между касатель
ными в двух точках кривой, лежащих на расстоянии Δs). Радиус кривизны − это радиус максимальной окружности, которую можно вписать в кривую в данной точке. Радиус кривизны окружности равен радиусу окружности, у прямой он равен ∞.
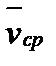
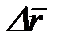

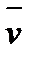
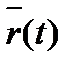
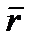 − вектор перемещения. Средней скоростью точки за время Δt называется вектор
− вектор перемещения. Средней скоростью точки за время Δt называется вектор 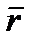 /Δt. Скоростью точки в данный момент времени называется предел, к которому стремится отношение вектора перемещения к промежутку времени, за которое оно произошло, при стремлении последнего к нулю :
/Δt. Скоростью точки в данный момент времени называется предел, к которому стремится отношение вектора перемещения к промежутку времени, за которое оно произошло, при стремлении последнего к нулю : 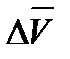
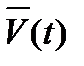
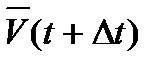
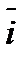 +y·
+y· 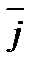 +z·
+z· 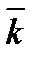 , тогда (т.к.
, тогда (т.к. 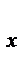 ·
· 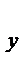 ·
· 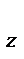 ·
· 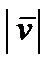 =
= 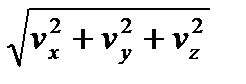 ,
а также направляющие косинусы:
соs(
,
а также направляющие косинусы:
соs( 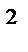 x / dt
x / dt 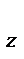 =dvz /dt =d
=dvz /dt =d 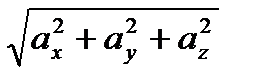 ; направляющие косинусы:
; направляющие косинусы: