
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Решение. Решение. Примем .. Решение. Задача 4.
Решение
1) Главные напряжения определяются по формуле:
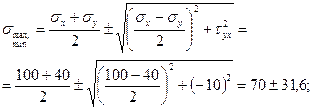
 ;
;
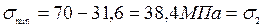 ;
;
направления главных площадок
 ;
;  .
.
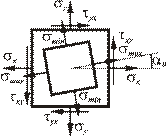
|
(Положительный угол отсчитывается против часовой стрелки. Максимальное нормальное напряжение проходит через ту четверть, где касательные напряжения сходятся). |
| Рис. |
2) Максимальное касательное напряжение равно
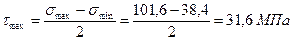 и действует на площадках, направленных под углом 45° к главным площадкам.
и действует на площадках, направленных под углом 45° к главным площадкам.
3) относительные линейные деформации находим, используя зависимости обобщенного закона Р.Гука (приняты: модуль упругости 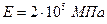 , коэффициент Пуассона
, коэффициент Пуассона 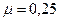 ).
).
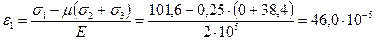 ;
;
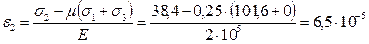 ;
;
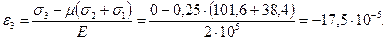 4) Относительное изменение объема
4) Относительное изменение объема 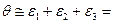
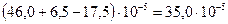 .
.
5) удельная потенциальная энергия деформация определяется по формуле:
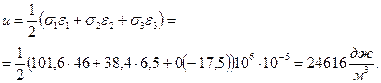 .
.
Задача 2.
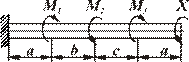
| Дано: Найти величины, требуемые по условию задачи. |
| Рис. |
Решение
1. Установим, при каком значении момента 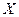 угол закручивания правого торцевого сечения равен нулю, т.е.
угол закручивания правого торцевого сечения равен нулю, т.е. 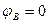 .
.
В соответствии с принципом независимости действия сил (ПНДС)
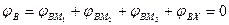 .
.
Но 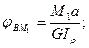
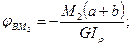
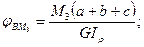
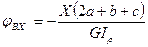 .
.
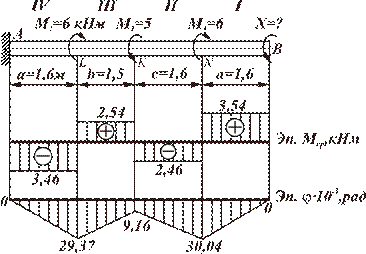
Отсюда
 и
и
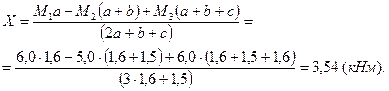
|
| Рис. |
2. Построим эпюру крутящих моментов
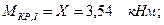

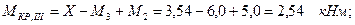
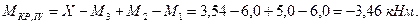
По эпюре крутящих моментов находим максимальный по модулю крутящий момент:
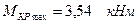 .
.
3. Определим из расчёта на прочность диаметр вала:
 ,
,
отсюда 
Для круглого сечения 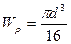 . Отсюда
. Отсюда 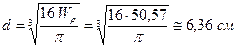 .
.
Примем .
Вычислим полярный момент инерции поперечного сечения вала:

Жёсткость поперечного сечения при кручении 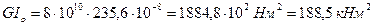 .
.
4. Построим эпюру углов закручивания.
4.1. Определим сначала углы закручивания на участках.
Расчётная формула: 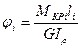 ;
;
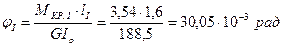 ;
;
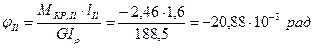 ;
;
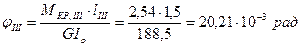 ;
;
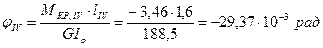 .
.
4.2 Эпюра углов закручивания:
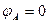 , т.к. сечение защемлено;
, т.к. сечение защемлено;
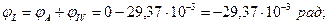

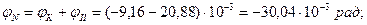
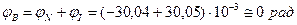 , что и должно быть по условию задачи.
, что и должно быть по условию задачи.
5. Максимальный относительный угол закручивания
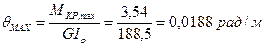 .
.
Задача 3. Для поперечного сечения, состоящего из швеллера № 16 и равнобокого уголка 100х100х12, определить положение главных центральных осей и значения главных моментов.
Решение
Вычерчиваем сечение в масштабе (рис.), для чего из таблицы сортамента берём следующие данные:
швеллер № 16: 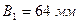 ,
, 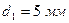 ;
; 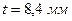 ;
; 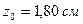 ;
; 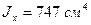 ;
;  ;
; 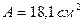 ;
;
уголок 80х50х6: 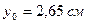 ;
; 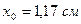 ;
; 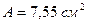 ;
; 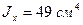 ;
; 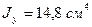 ;
; 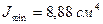
 .
.
Показываем положение центров тяжести (точки 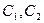 ) каждой фигуры, через которые проводим оси
) каждой фигуры, через которые проводим оси 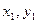 и
и 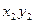 .
.
Следует обратить внимание на то обстоятельство, что положение уголка в заданном сечении не соответствует положе-нию в сортаменте. Поэтому 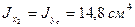 , а
, а 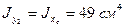 , где
, где 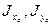 -моменты инерции относительно осей
-моменты инерции относительно осей  , применяемых в сортаменте.
, применяемых в сортаменте.
Для определения положения центра тяжести сечения выбираем произвольную систему координат 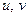 , в которой положение центров тяжести отдельных элементов легко определяется. В данном примере оси проведены по наружному контуру стенки и нижней полки швеллера. Однако можно выбрать любое другое положение осей.
, в которой положение центров тяжести отдельных элементов легко определяется. В данном примере оси проведены по наружному контуру стенки и нижней полки швеллера. Однако можно выбрать любое другое положение осей.
Координаты центра тяжести вычисляем по формулам:

 ,
,
где
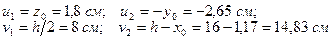
Показываем положение центра тяжести всего сечения – т. 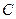 и проводим центральные оси
и проводим центральные оси  . Cледует подчеркнуть, что для сечения, состоящего из двух фигур, общий центр тяжести располагается на прямой
. Cледует подчеркнуть, что для сечения, состоящего из двух фигур, общий центр тяжести располагается на прямой  , соединяющей центры тяжести отдельных фигур.
, соединяющей центры тяжести отдельных фигур.
Для вычисления моментов инерции относительно центральных осей  используем зависимость:
используем зависимость:
 ;
;
здесь
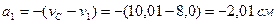 ;
;
 .
.
 ,
,
здесь

Для определения центробежного момента инерции всего сече-ния 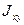 вначале определяем центробежный момент инерции угол-ка относительно собственных центральных осей
вначале определяем центробежный момент инерции угол-ка относительно собственных центральных осей 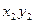 .
.
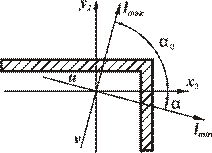
| В сортаменте для уголка |
| Рис. |
Тогда 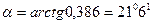 , а угол
, а угол 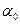 между горизонтальной осью и осью, момент инерции относительно которой равен
между горизонтальной осью и осью, момент инерции относительно которой равен 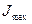 , является дополнительным, то есть
, является дополнительным, то есть 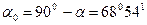 . В данном случае угол
. В данном случае угол 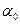 является положительным, так как откладывается против часовой стрелки.
является положительным, так как откладывается против часовой стрелки.
Используя уравнение для заданного по условию задачи положения уголка, можно получить
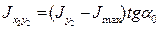 ,
,
а, учитывая, что 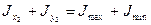 , получаем
, получаем
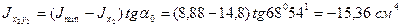 .
.
Центробежный момент инерции всего сечения относи-тельно осей 
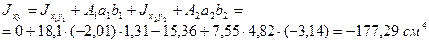

|
| Рис. |
Вычисляем главные моменты инерции
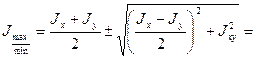
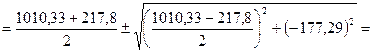
 ;
;
Окончательно имеем
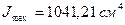 ,
, 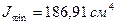
Положение главной оси, относительно которой момент инерции равен 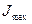 , определим по формуле (2.15)
, определим по формуле (2.15)

Тогда 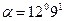 , а так как угол положительный, то на рис. откладываем его против часовой стрелки.
, а так как угол положительный, то на рис. откладываем его против часовой стрелки.
Задача 4.
Схема а)

| Дано:
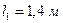 ; ;  ; ; 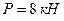 ; ; 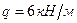 .
Подобрать сечение .
Подобрать сечение
|
| Рис. |
Решение
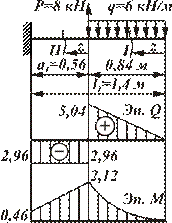
1. Балка консольная, поэтому можно опорные реакции не определять. Балка имеет два участка. Эпюры внутренних усилий строим, используя метод сечений – РОЗУ.
Участок 1.  .
.
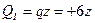 – линейная функция; ее график – наклонная прямая.
– линейная функция; ее график – наклонная прямая.
| При При
При При
Участок 2.
|
| Рис. |
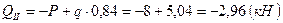 – график – прямая, параллельная оси.
– график – прямая, параллельная оси.
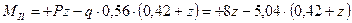 – наклонная прямая.
– наклонная прямая.
При 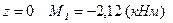 ;
;
При 
По эпюре М находим опасное сечение: сечение, в котором возникает максимальный по модулю изгибающий момент. Здесь 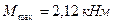
2. Условие прочности при изгибе: 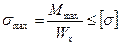 .
.
Из него определим требуемый момент сопротивления
 .
.
Для круглого сечения осевой момент сопротивления 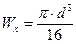 . Отсюда при известном моменте сопротивления
. Отсюда при известном моменте сопротивления 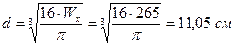 . Примем
. Примем 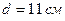 ?
?
Схема б)
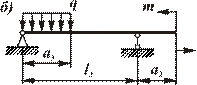 Рис.
Рис.
| Дано:
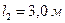 , ,  , , 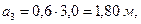  , , 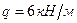 .
Подобрать сечение .
Подобрать сечение
|
Решение
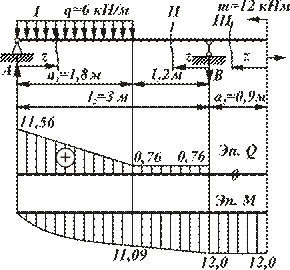
1. Определим  опорные реакции:
опорные реакции:
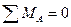 ;
; 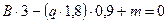 ;
;
 ;
;
– знак «-» указывает на то, направление реакции необходимо изменить на противоположное.
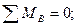
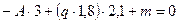 ;
;
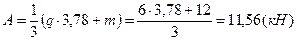 .
.
Контроль: 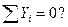
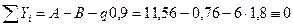 – реакции найдены верно.
– реакции найдены верно.
1. Балка имеет три участка. Используем метод сечений.
2а. Участок I.
 ;
;
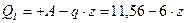 ; – поперечная сила на участке изменяется по линейному закону, график – наклонная прямая
; – поперечная сила на участке изменяется по линейному закону, график – наклонная прямая
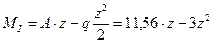 –квадратная функция;
–квадратная функция;
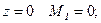
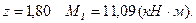
2б. Участок 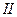 .
. 
|
| Рис. |
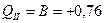 – поперечная сила постоянна.
– поперечная сила постоянна.
 – линейная функция;
– линейная функция;
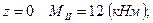
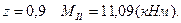
2в. Участок  .
.
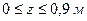 ;
;
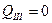 ;
;
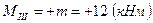 – момент постоянен на участке.
– момент постоянен на участке.
По эпюре М находим опасное сечение: сечение, в котором возникает максимальный по модулю изгибающий момент. Здесь 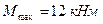
- Условие прочности при изгибе имеет вид:
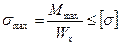 . Из него имеем
. Из него имеем 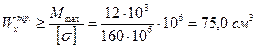 .
.
По сортаменту находим двутавр, имеющий осевой момент сопротивления, близкий к требуемому. Это двутавр №14с 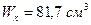 .
.
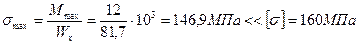
Недонапряжение  (при норме
(при норме 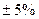 ), но для прокатных профилей такой процент недонапряжения допускается. Такое перенапряжение недопустимо. Приходится брать двутавр №14 с
), но для прокатных профилей такой процент недонапряжения допускается. Такое перенапряжение недопустимо. Приходится брать двутавр №14 с 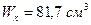 , что значительно больше требуемого.
, что значительно больше требуемого.
Ответ: двутавр № 14.
Задача 5

| Дано: Р=1000 кН. Подобрать сечение стойки.
Решение 1.
Отсюда площадь поперечного сечения
Попытка 1. Примем
Размер |
| Рис. |
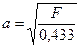 =
= 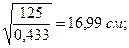 примем
примем 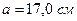 .
.
Площадь 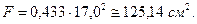
Найдём фактическое значение коэффициента продольного изгиба 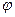 .
.
Гибкость стержня 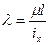 , здесь
, здесь  – главный радиус инерции,
– главный радиус инерции, 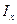 – осевой момент инерции сечения, для треугольника
– осевой момент инерции сечения, для треугольника
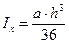 . Получаем
. Получаем
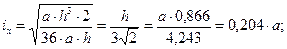
При 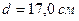
 .
.
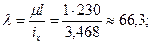 Определим, чему равен коэффициент продольного изгиба
Определим, чему равен коэффициент продольного изгиба 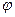 при такой гибкости.
при такой гибкости.
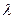
| 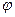
|
| 0,805 | |
| 0,754 | |
| 66,3 | 0,773 |
Получен 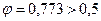 , результат неудовлетворительный.
, результат неудовлетворительный.
Попытка 2.Примем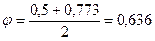
 сторона равностороннего треугольника
сторона равностороннего треугольника 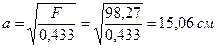 ¸ примем
¸ примем 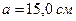 .
.
Найдём фактическое значение коэффициента продольного изгиба 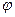 .
.
Гибкость стержня 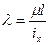 . Радиус инерции
. Радиус инерции 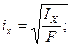
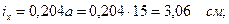
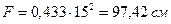

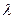
| 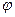
|
| 0,754 | |
| 0,686 | |
| 75,2 | 0,719 |
0,719>0,636, но, тем не менее, проверим, как выполняется условие устойчивости:
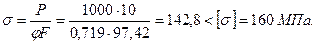 Недонапряжение:
Недонапряжение: 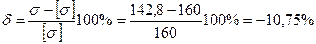 – недопустимо (норма
– недопустимо (норма 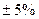 ).
).
Попытка 3.Примем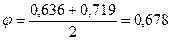 .
.
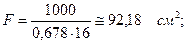
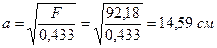 ¸ примем
¸ примем 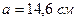
Коэффициент продольного изгиба 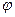 =?
=?
Радиус инерции 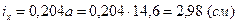 , площадь сечения
, площадь сечения 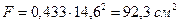
Гибкость стержня 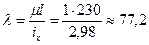
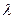
| 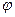
|
| 0,754 | |
| 0,686 | |
| 77,2 | 0,705 |
0,705>0,678.
Проверим, как выполняется условие устойчивости:

Недонапряжение: 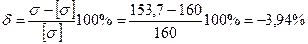 , что в пределах нормы (норма
, что в пределах нормы (норма 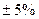 ).
).
2. Гибкость стержня при 
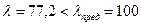 , следовательно, формула Л. Эйлера
, следовательно, формула Л. Эйлера 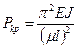 не справедлива. Применяем формулу Ясинского
не справедлива. Применяем формулу Ясинского  ,
,
где а = 310 и 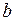 = 1,14 определяются по справочнику.
= 1,14 определяются по справочнику.
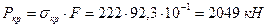 ,
,
коэффициент запаса устойчивости 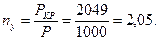
Рекомендуемая литература
1. Александров А.В., Потапов В.Д., Державин Б.П. Сопротивление материалов: Учебник для вузов – М.: Высшая школа, 2004 – 560 с.
2. Ицкович Г.М., Минин Л.С., Виноградов А.И. Руководство к решению задач по сопротивлению материалов: Учебное пособие для вузов – М.: Высшая школа, 2001 – 592 с.
3. Феодосьев В.И. Сопротивление материалов: Учебник для вузов – М.: Издательство МГТУ им. Н.Э. Баумана, 1999 – 592 с.
4. Сопротивление материалов. Учебное пособие. Под редакцией Н.А. Костенко. – М.: Высшая школа, 2004 – 430 с.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|
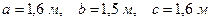 ;
; 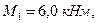
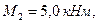
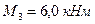 ;
; 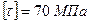 .
.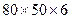 задан
задан 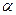 - угол между главной осью
- угол между главной осью 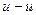 , момент инерции относительно которой равен
, момент инерции относительно которой равен  , и осью
, и осью 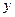 , которая для заданного положения уголка совпадает с осью
, которая для заданного положения уголка совпадает с осью 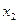 .
.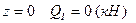 ;
;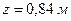
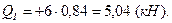
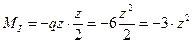 – квадратная парабола.
– квадратная парабола. ;
;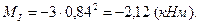
 .
. Условие устойчивости центрально сжатого стержня имеет вид:
Условие устойчивости центрально сжатого стержня имеет вид: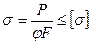 .
.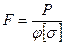 .
.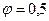 ,
,  тогда площадь сечения
тогда площадь сечения 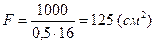 , но
, но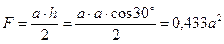 ;
;