Показатели эксцесса (островершинности).

Показатели эксцесса (островершинности).

Показатели эксцесса рассчитываются для симметричных распределений.

Наиболее точным показателем эксцесса является показатель определяемый по формуле:

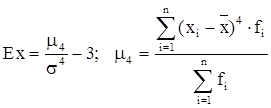
Эксцесс может быть положительным и отрицательным. У островершинных распределений показатель эксцесса имеет положительный знак, а у плосковершинных - отрицательный знак. Предельным значением отрицательного эксцесса является Ex=-2; величина положительного эксцесса является величиной бесконечной. В нормальном распределении Ex=0.

Для приближенного определения величины эксцесса может быть использована формула Линдберга:

Ex=П - 38.29,

где П - процент количества вариант, лежащих в интервале, равном половине среднего квадратического отклонения (в ту и другую сторону от величины средней).

3. Критерии согласия.

В статистической практике большой интерес представляет решение вопроса о степени соответствии полученного в результате статистического наблюдения эмпирического распределения теоретическому.

Решение данного вопроса производится с помощью особых показателей - критериев согласия.

Критерии согласия основаны на использовании различных мер расстояний между анализируемым эмпирическим распределением и функцией теоретического распределения.

Наиболее распространенным является критерий согласия Пирсона c² (“хи-квадрат”), вычисляемый по формуле:

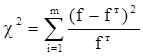Полученное значение критерия ( 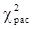) сравнивается с табличным значением ( ). Последнее определяется по специальной таблице в зависимости от принятой вероятности (Р) и числа степеней свободы k. Число степеней свободы равно: k=m-l-1, где m - число групп, l - число параметров в уравнении теоретического распределения (в случае нормального распределения - l =2, в случае распределения Пуассона- l =1 ).

Если 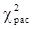£ , то эмпирическое распределение соответствует теоретическому.

При расчете критерия Пирсона нужно соблюдать следующие условия:

· число наблюдений должно быть достаточно велико (n ³ 50);

· если теоретические частоты в некоторых интервалах меньше 5, то такие интервалы объединяют так, чтобы частоты были более 5.

Используя величину c², В.И. Романовский предложил оценку близости эмпирического распределения кривой нормального распределения производить следующим образом: если 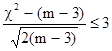, то гипотеза о подчинении эмпирического распределения нормальному закону принимается, иначе - отвергается.

Распространенным критерием согласия является критерий А.И. Колмогорова:

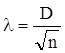где D - максимальное значение разности между накопленными эмпирическими и теоретическими частотами.

По таблице значений вероятности находят соответствующую вероятность Р(l). Если величина вероятности, соответствующая l, является значительной, то расхождение между эмпирическим и теоретическим распределениями несущественны.

⇐ Предыдущая 1 23