Показатели формы распределения.

2. Показатели формы распределения.

Выяснение общего характера распределения предполагает оценку степени его однородности, а также вычисления показателей формы распределения.

Показатели асимметрии.

Симметричным является распределение, в котором частоты любых двух вариант, равноотстоящих в обе стороны от центра распределения, равны между собой.

Для симметричных распределений средняя арифметическая, мода и медиана равны между собой. В связи с этим простейший показатель асимметрии основан на соотношении показателей центра распределения: чем больше разница (`x - Mо), тем больше асимметрия распределения.

Для сравнительного анализа степени асимметрии нескольких распределений рассчитывают относительный показатель As:

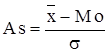Величина показателя асимметрии As может быть положительной и отрицательной. Положительная величина показателя асимметрии указывает на наличие правосторонней асимметрии. Отрицательный знак показателя асимметрии говорит о наличии левосторонней асимметрии. Чем больше абсолютная величина коэффициента, тем больше асимметрия. Принято считать, что если коэффициент асимметрии по модулю меньше 0.25, то асимметрия незначительная, если свыше 0.5, то значительная.

Другой показатель асимметрии предложен шведским математиком Линдбергом:

As=П - 50,

где П - процент значений признака, превышающих величину средней арифметической.

Наиболее точным и распространенным является показатель асимметрии, вычисляемый по формуле:

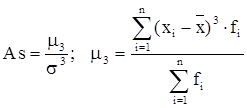Оценка степени существенности этого показателя производится с помощью средней квадратической ошибки:

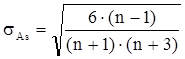Если 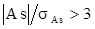- асимметрия существенна

Если 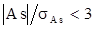- асимметрия несущественна.

⇐ Предыдущая 123 Следующая ⇒