
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Конспект лекций 4 страница
Физический смысл теоремы Гаусса для вектора 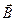 заключается в следующем: в природе нет магнитных зарядов и поэтому линии
заключается в следующем: в природе нет магнитных зарядов и поэтому линии 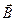 являются замкнутыми
являются замкнутыми
Работа по перемещению проводника и контура с током в магнитном поле
1) Элементарный магнитный поток( 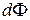 ):
):
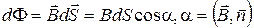 ;
;
2) Элементарная работа по перемещению проводника (контура) с током в магнитном поле : 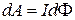
3) Работа по перемещению проводника (контура) с током в магнитном поле : 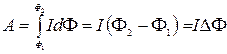 ;
;
4) Магнитный момент контура с током: 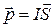 , где
, где 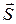 - площади контура;
- площади контура;
4) Потенциальной энергии проводника (контура) с током в магнитном поле: 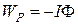 или
или 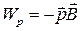 ;
;
Движение заряженных частиц в электрическом и магнитном полях
1) Движение в однородном магнитном поле
Со стороны магнитного поля на движущуюся в нем заряженную частицу действует сила Лоренца ( 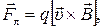
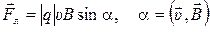 ), создающая только нормальное ускорение.
), создающая только нормальное ускорение.
· α=0. В этом случае 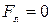 , частица движется прямолинейно вдоль линий вектора
, частица движется прямолинейно вдоль линий вектора 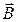 .
.
· α=p/2. Частица движется в магнитном поле перпендикулярно линиям вектора 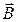 . Траектория движения частицы - окружность радиуса R. Используя второй закон Ньютона, для радиуса R и периода Т обращения частицы можно получить
. Траектория движения частицы - окружность радиуса R. Используя второй закон Ньютона, для радиуса R и периода Т обращения частицы можно получить
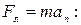
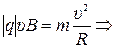
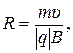
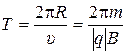
· α – произвольный угол.Траектория движения частицы - винтовая линия. Движение частицы можно представить как сумму двух видов движения - прямолинейного вдоль линий 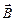 (α=0) и движения по окружности в плоскости, перпендикулярной вектору
(α=0) и движения по окружности в плоскости, перпендикулярной вектору 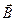 (α=p/2).
(α=p/2).
Радиус окружности R, период обращения Т и шага h винтовой линии определяются выражениями:
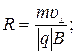
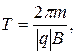
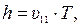
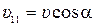 ,
, 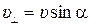 .
.
2) Движение в скрещенных электрическом и магнитном полях
В скрещенных под прямым углом однородных электрическом ( 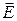 ) и магнитном (
) и магнитном ( 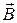 ) полях заряженная частица будет двигаться равномерно и прямолинейно, если ее вектор скорости
) полях заряженная частица будет двигаться равномерно и прямолинейно, если ее вектор скорости 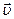 будет оюразовывать левую тройку векторов с
будет оюразовывать левую тройку векторов с 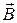 и
и 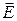 , а модуль вектора скорости равен:
, а модуль вектора скорости равен: 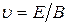 (т.к. в этих условиях
(т.к. в этих условиях 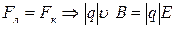 ).
).
3) Эффект Холла
При протекании электрического тока. На движущиеся свободные электрические заряды (электроны или «дырки») со стороны внешнего магнитного поля будет действовать сила Лоренца, которая приведёт к движению электронов («дырок») к верхней (нижней) грани образца. В результате этого верхняя грань образца зарядится отрицательно (положительно), а нижняя – положительно (отрицательно) и возникает поперечное электрическое поле, напряжённость 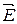 которого будет перпендикулярна векторам
которого будет перпендикулярна векторам 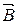 и
и 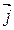 . В возникновении поперечного электрического поля в образце при помещении его в магнитное поле при протекании в нем электрического тока и заключается эффект Холла.
. В возникновении поперечного электрического поля в образце при помещении его в магнитное поле при протекании в нем электрического тока и заключается эффект Холла.
Разность потенциалов в эффекте Холла 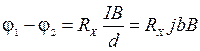
Формула для постоянной Холла 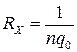 , где n и q0 – концентрация и электрический заряд носителей тока (подвижных зарядов) в образце.
, где n и q0 – концентрация и электрический заряд носителей тока (подвижных зарядов) в образце.
Электромагнетизм
Явление и закон электромагнитной индукции
1) Закон Фарадея. При всяком изменении магнитного потока, пронизывающего проводящий контур, в нём возникает э.д.с. индукции ei , равная скорости изменения магнитного потока, связанного с этим контуром, взятой с обратным знаком.
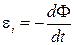 ;
;
2) Правило Ленца. Индукционный ток в контуре возникает такого направления, чтобы создаваемое им магнитное поле препятствовало любым изменениям магнитного потока, вызвавшего этот индукционный ток.
3) Первое положение теории Максвелла: переменное во времени магнитное поле порождает в окружающем пространстве вихревое электрическое поле. В отличие от электростатического поля линии вихревого электрического поля являются замкнутыми, они связаны с направлением вектора 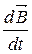 правилом левого буравчика и лежат в плоскости, перпендикулярной к вектору
правилом левого буравчика и лежат в плоскости, перпендикулярной к вектору 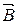 . Силы вихревого электрического поля – сторонние силы;
. Силы вихревого электрического поля – сторонние силы;
4) Работа сил вихревого электрического поля
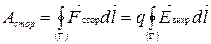 ;
;
5) Первое уравнение Максвелла в интегральной форме: 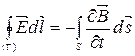 . Физический смысл первого уравнения Максвелла: источником вихревого электрического поля является переменное магнитное поле;
. Физический смысл первого уравнения Максвелла: источником вихревого электрического поля является переменное магнитное поле;
6) Токи Фуко – это индукционные токи, возникающие в массивных проводниках;
12) Скин-эффект явление неравномерного распределения переменного тока по поперечному сечению проводника, повышение его плотности в поверхностном слое;
Явление самоиндукции
1) Магнитный поток самоиндукции ( 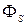 ) – магнитный поток, связанный с проводящим контуром, и, создаваемый (вследствие закона Био-Савара-Лапласа) электрическим током, текущим по этому контуру;
) – магнитный поток, связанный с проводящим контуром, и, создаваемый (вследствие закона Био-Савара-Лапласа) электрическим током, текущим по этому контуру;
2) Потокосцепление (Ψ) – произведения числа витков N на магнитный поток, пронизывающий один виток: 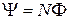 ;
;
3) Индуктивность контура: 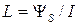 ;
;
4) Индуктивность длинного соленоида: 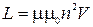 ;
;
5) Закон самоиндукции. При всяком изменении тока, текущего по проводнику, э.д.с. самоиндукции ei , равная скорости изменения потокосцепления, взятой с обратным знаком.
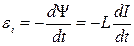 .
.
Таким образом, явление самоиндукции заключается в возникновении э.д.с. индукции в проводящем контуре при изменении силы тока, текущего в нём;
6) Правило Ленца для явления самоиндукции – ток самоиндукции препятствует любым изменениям основного тока, текущего по цепи.
Экстра токи (токи при замыкании и размыкании цепи)
При размыкании цепи ток в ней начинает убывать. Он убывает постепенно за счёт возникающего в цепи явления самоиндукции. При этом запасённая в катушке энергия магнитного поля расходуется на поддержание убывающего тока, расходуется на нагревание проводников. В случае замыкания цепи – ток в ней будет нарастать постепенно по той же причине.
1) Зависимость силы тока от времени при размыкании цепи:
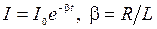 , R и L – сопротивление и индуктивность цепи;
, R и L – сопротивление и индуктивность цепи;
2) Зависимость силы тока от времени при замыкании цепи:
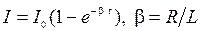 , R и L – сопротивление и индуктивность цепи;
, R и L – сопротивление и индуктивность цепи;
3) Зависимость э.д.с. самоиндукции от времени t при размыкании цепи:
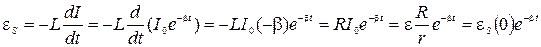 ,
,
где R и r – сопротивление цепи и внутреннее сопротивление источника тока, а 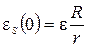 .
.
Энергия магнитного поля
1) Энергия магнитного поля контура с током: 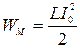 ;
;
2) Объёмная плотность энергии магнитного поля: 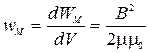 ;
;
3) Энергия магнитного поля, заключённая в конечном объёме V:
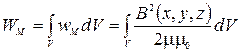 .
.
Второе уравнение Максвелла в интегральной форме. Ток смещения
1) Второе положение теории Максвелла: переменное электрическое поле порождает в окружающем пространстве магнитное поле;
2) Второе уравнение Максвелла в интегральной форме следующего вида:
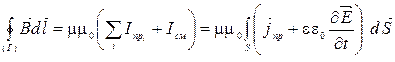 ;
;
3) Ток смещения(Iсм) – скалярная физическая величина, измеряемая в амперах, характеризующая способность электрического поля создавать магнитное поле и пропорциональная скорости изменения во времени напряжённости 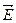 электрического поля:
электрического поля: 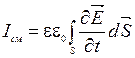 .
.
4) Плотность тока смещения: 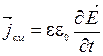 ;
;
Система уравнений Максвелла
1) В интегральной форме:
1. 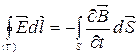 , 2.
, 2. 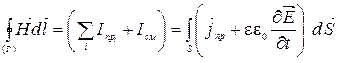 ,
,
3. 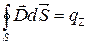 , 4.
, 4. 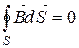 ,
,
5. 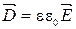 . 6.
. 6. 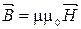 . 7.
. 7. 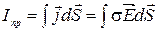 .
.
2) В дифференциальной форме:
1. 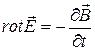 2.
2. 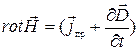
3. 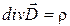 4.
4. 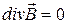
5. 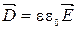 . 6.
. 6. 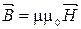 . 7.
. 7. 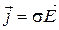 .
.
Магнитное поле в веществе
Все вещества являются магнетиками, т.е. при помещении их во внешнее магнитное поле 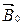 они создают своё собственное магнитное поле
они создают своё собственное магнитное поле 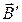 , т.е. намагничиваются. В результате чего магнитное поле в веществе определяется выражением:
, т.е. намагничиваются. В результате чего магнитное поле в веществе определяется выражением: 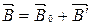 ;
;
1) Магнитная проницаемость вещества (μ): 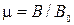 ;
;
2) Вектор намагничивания или намагниченность ( 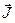 ) – магнитный момент единицы объема вещества:
) – магнитный момент единицы объема вещества:
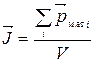 ;
;
3) Магнитный момент атома: 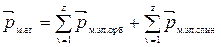 ;
;
3) Вектор напряженности магнитного поля ( 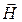 ):
):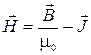 .
.
Формула связи 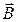 и
и 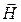 :
: 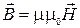 ;
;
4) Магнитная восприимчивость вещества (χ): 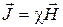 .
.
Формула связи μ и χ: 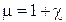 ;
;
5) Теорема о циркуляции вектора намагниченности: 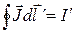 ;
;
6) Теорема о циркуляции вектора напряженности магнитного поля:
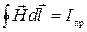 .
.
Магнетики
1) Диамагнетики – вещества, у которых в отсутствии внешнего магнитного поля магнитный момент атома равен нулю. Для них магнитная восприимчивость не зависит от индукции внешнего магнитного поля, принимает малые по модулю отрицательные значения c 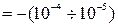 ,
,
2) Диамагнитный эффект – возникновение индуцированного магнитного момента атома 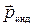 , направленного противоположно внешнему магнитному полю
, направленного противоположно внешнему магнитному полю 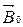 , свойственен всем веществам, но для остальных групп магнетиков он не учитывается ввиду его малости.
, свойственен всем веществам, но для остальных групп магнетиков он не учитывается ввиду его малости.
3) Парамагнетики – вещества, у которых в отсутствии внешнего магнитного поля магнитный момент атома отличен от нуля. Для них магнитная восприимчивость c не зависит от модуля 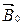 , и принимает малые числовые значения c=(10-3-10-2)>0.
, и принимает малые числовые значения c=(10-3-10-2)>0.
4) Закон Кюри, описывающий изменение магнитной восприимчивости парамагнетика от температуры: 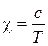 .
.
5) Магнитоупорядоченные вещества (ферро-, антиферро- и ферримагнетики) – вещества, у которых в отсутствии внешнего магнитного поля магнитный момент атома не равен нулю. В отличие от парамагнетиков для них магнитная восприимчивость существенно зависит от индукции 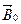 внешнего магнитного поля.
внешнего магнитного поля.
Основные особенности ферромагнетиков:
6) Спонтанная намагниченность – определяющая особенность ферромагнетиков, заключающаяся в том, что в отсутствии внешнего магнитного поля магнитные моменты их атомов не равны нулю и вследствие взаимодействия ориентируются в одном направлении при температурах ниже некоторого критического значения, получившего название температура Кюри (TC). По этой причине в отсутствии внешнего магнитного поля и при T<TC намагниченность этих веществ не равна нулю
7) Температура Кюри – температура выше которой ферромагнетик теряет свои необычные свойства и становится обычным парамагнетиком;
8) Явление гистерезиса – зависимость свойств образца от его предшествующих состояний или явление отставания изменения намагниченности от изменения внешнего магнитного поля большие значения магнитных моментов атомов;
9) Домены – области внутри ферромагнетика магнитный момент которых не равен нулю (из-за соноправленности магнитных моментов атомов, расположенных в этих областях);
10) Закон Кюри-Вейсса: 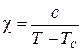 , описывает температурную зависимость магнитной восприимчивости ферромагнетиков при T>TC;
, описывает температурную зависимость магнитной восприимчивости ферромагнетиков при T>TC;
Модуль 5: Электромагнитные колебания и влны. Волновая оптика
Электромагнитные колебания
1) Колебательный контур состоит из катушки индуктивностью L, конденсатора емкости С и сопротивления R;
2) Электромагнитные колебания (ЭМК) в колебательном контуре – колебания электрического заряда 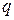 , напряжения на конденсаторе
, напряжения на конденсаторе 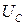 и катушке индуктивности
и катушке индуктивности 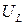 , силы тока
, силы тока 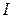 , энергии магнитного поля катушки
, энергии магнитного поля катушки 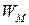 и энергии электрического поля конденсатора
и энергии электрического поля конденсатора 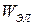 , векторов электрического поля конденсатора
, векторов электрического поля конденсатора 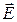 и вектора магнитной индукции магнитного поля
и вектора магнитной индукции магнитного поля 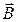 катушки, происходящие в колебательном контуре;
катушки, происходящие в колебательном контуре;
3) Дифференциальное уравнение ЭМК в колебательном контуре
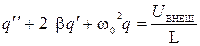 ,
,
где 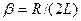 - коэффициент затухания, а
- коэффициент затухания, а 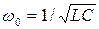 - циклическая (круговая) частота свободных незатухающих гармонических колебаний.
- циклическая (круговая) частота свободных незатухающих гармонических колебаний.
| Механические колебания | Электромагнитные колебания в контуре |
| Смещение х | Электрический заряд q |
Проекция скорости 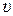 x= x= 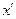
| Сила тока I= 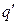
|
| Масса тела m | Индуктивность катушки L |
| Коэффициент жесткости системы k | Обратная электроемкость конденсатора 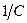
|
| Коэффициент сопротивления среды r | Активное сопротивление R |
Электромагнитные волны
Основные понятия и определения:
1) Система уравнений Максвелла в вакууме ( 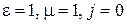 ):
):
1. 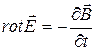 2.
2. 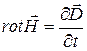
3. 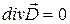 4.
4. 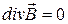
5. 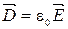 . 6.
. 6. 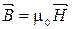 .
.
2) Волновые уравнения для плоской монохроматической ЭМВ:
волны электрического поля: – 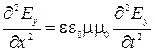 ,
,
волны магнитного поля: – 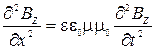 ;
;
3) Уравнения плоских монохроматических волн электрического и магнитного полей: 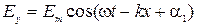 ,
, 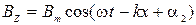 ;
;
4) Фазовая скорость ЭМВ: 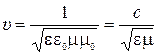 , где с – скорость ЭМВ в вакууме равная (совпадающая) скорости света в вакууме;
, где с – скорость ЭМВ в вакууме равная (совпадающая) скорости света в вакууме;
5) Скорость и длина волны ЭМВ: 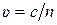 ,где
,где 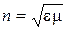 - показатель преломления среды;
- показатель преломления среды; 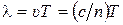 Þ
Þ 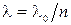 , где
, где 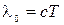 - длина волны в вакууме,
- длина волны в вакууме,
6) Свойства ЭМВ:
а) Скорость ЭМВ в вакууме не зависит от частоты и равна скорости света в вакууме ( 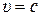 );
);
б) .Фазы колебаний векторов 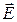 и
и 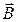 ЭМВ совпадают;
ЭМВ совпадают;
в) ЭМВ является поперечной и плоско поляризованной;
г) Вектора 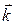 ,
, 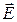 и
и 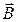 – взаимно перпендикулярны и образуют левую тройку векторов.
– взаимно перпендикулярны и образуют левую тройку векторов.
Объемные плотности энергии ЭМВ. Вектор Умова-Пойнтинга
1) Объемная плотность энергии электрического и магнитного полей ЭМВ – равны: 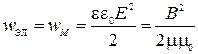 ;
;
2) Объемная плотность энергии ЭМВ:
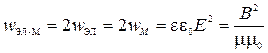 ;
;
3) Вектор Умова-Пойнтинга ( 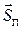 ) – вектор плотности потока энергии ЭМВ:
) – вектор плотности потока энергии ЭМВ:
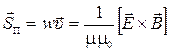 ;
;
4) Усредненная по времени объемная плотность ЭМВ:
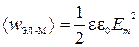 ;
;
5) Интенсивность ЭМВ: 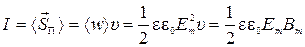 ;
;
6) Мощность излучения ЭМВ (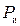 )и средняя мощность ЭМВ (
)и средняя мощность ЭМВ (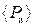 ), излучаемой каким-либо источником:
), излучаемой каким-либо источником:
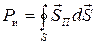 и
и 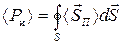 .
.
Отражение ЭМВ на границе сред.
При отражении плоской ЭМВ от оптически более плотной среды ( 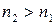 ) происходит изменение фазы колебаний вектора
) происходит изменение фазы колебаний вектора 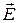 на
на 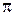 (вектора
(вектора 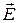 и
и 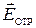 направлены в противоположные стороны). При этом изменение фазы вектора
направлены в противоположные стороны). При этом изменение фазы вектора 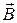 не происходит (вектора
не происходит (вектора 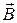 и
и 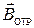 сонаправлены).
сонаправлены).
При отражении от оптически менее плотной среды ( 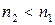 ) изменение фазы колебаний вектора
) изменение фазы колебаний вектора 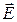 не происходит, а фаза вектора
не происходит, а фаза вектора 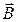 изменяется на
изменяется на 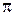 .
.
Это означает, что при отражении падающей на границу раздела двух сред плоской электромагнитной волны тройка векторов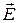 ,
, 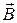 и
и 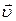 поворачивается на угол 1800 либо вокруг вектора
поворачивается на угол 1800 либо вокруг вектора 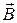 (
( 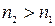 ), либо вокруг вектора
), либо вокруг вектора 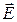 (
( 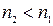 ).
).
Излучение ЭМВ диполем
1) Амплитуда сферической ЭМВ: 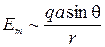 , где q-модуль одного из зарядов диполя, a - амплитуда ускорения, с которым движется отрицательный заряд (
, где q-модуль одного из зарядов диполя, a - амплитуда ускорения, с которым движется отрицательный заряд ( 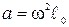 ), угол θ – угол между осью диполя и вектором
), угол θ – угол между осью диполя и вектором 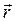 , проведенным от диполя в рассматриваемую точку пространства;
, проведенным от диполя в рассматриваемую точку пространства;
2) Мощность ЭМВ, излучаемой диполем:
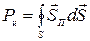 ~
~ 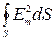 ~
~ 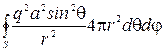 ~
~ 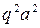 ~
~ 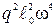 ~
~ 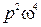 .
.
3) Интенсивность ЭМВ, излучаемой диполем: 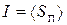 ~
~ 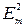 ~
~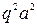 ~
~ 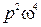
4) Диаграмма излучения диполя: 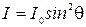 ;
;
Волновая оптика
Основные понятия и определения:
Видимый свет – ЭМВ с длинами волн, лежащими в диапазоне от 400 нм до 780 нм (ω=(2,42÷4,71) 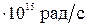 ). Такие волныиспускаются при переходах электронов между уровнямиэнергий в молекулах и атомах, при тепловых и электрических воздействиях на них.
). Такие волныиспускаются при переходах электронов между уровнямиэнергий в молекулах и атомах, при тепловых и электрических воздействиях на них.
В этом диапазоне излучения глаз человека различает такие основные цвета, как фиолетовый, синий, голубой, зеленый, желтый, оранжевый, красный. Любой цвет можно получить сложением трех независимых цветов в качестве которых можно взять, например, синий, красный и зеленый. Если сложить все волны видимого диапазона излучения, то тогда получится излучение, которое называют белым светом.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|