
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Конспект лекций 2 страница
Механические колебания и волны
Колебания – повторяющийся во времени процесс изменения физической величины.
Волна – процесс распространения колебаний в пространстве
Гармонические колебания
Основные понятия и определения:
1) гармоническое колебание – колебание, происходящее по закону синуса или косинуса;
2) уравнение гармонических колебаний: 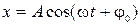 , где
, где 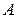 – амплитуда колебаний,
– амплитуда колебаний, 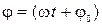 – фаза колебаний,
– фаза колебаний, 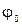 – начальная фаза колебаний,
– начальная фаза колебаний, 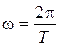 – циклическая (круговая) частота;
– циклическая (круговая) частота;
3) Период колебаний (Т) – минимальное время возвращения колеблющейся системы в исходное состояние (или время одного полного колебания);
4) Свободные незатухающие гармонические колебания. Дифференциальное уравнение:
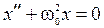
и его решение: 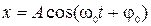 ;
;
5) Сила сопротивления: 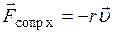
6) Затухающие колебания. Дифференциальное уравнение:
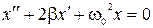
и его решение: 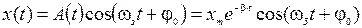 , где
, где 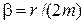 ,
, 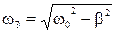 – частота затухающих колебаний,
– частота затухающих колебаний, 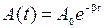 – амплитуда затухающих колебаний;
– амплитуда затухающих колебаний;
7) Время релаксации ( 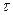 ) – время за которое амплитуда затухающих колебаний убывает
) – время за которое амплитуда затухающих колебаний убывает 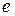 раз (
раз ( 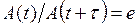 )
)
8) Логарифмический декремент затухания (δ): 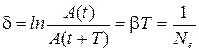 , где
, где 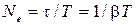 – число колебаний за время релаксации;
– число колебаний за время релаксации;
9)Добротность системы(Q):
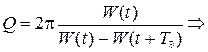
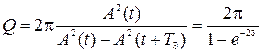
18) Вынужденные гармонические колебания. Дифференциальное уравнение:
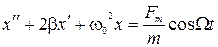
и его решение в стационарном режиме:  , где
, где 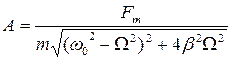 и
и 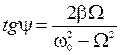 ,
, 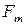 и
и 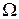 – амплитуда и циклическая частота внешней вынуждающей силы;
– амплитуда и циклическая частота внешней вынуждающей силы;
Основные формулы и соотношения:
1) Собственная частота колебаний:
· пружинный маятник – 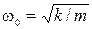 ,
,
· математический маятник 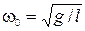 ,
,
· физический маятник 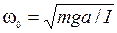 , m – масса физического маятника, а – расстояние между точкой подвеса и центром масс, I – момент инерции физического маятника относительно центра масс;
, m – масса физического маятника, а – расстояние между точкой подвеса и центром масс, I – момент инерции физического маятника относительно центра масс;
2) Приведенная длина физического маятника 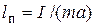 ;
;
3) Условия малого затухания:
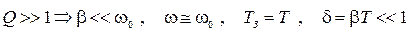
4) Добротность в условиях малого затухания:
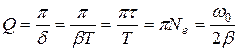 ,
, 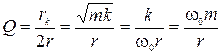
5) зависимость полной энергии затухающих колебаний от времени:
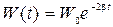 ;
;
6) Уравнение резонансной кривой для амплитуды смещения:
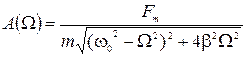 ;
;
7) Уравнение резонансной кривой для амплитуды скорости:
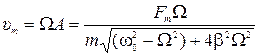 ;
;
8) Резонансная частота для амплитуды смещения: 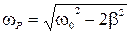 ;
;
9) формулы для амплитуды колебаний смещения материальной точки от положения равновесия при резонансе 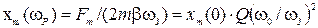 ;
;
10) формулы для 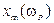 в условиях малого затухания:
в условиях малого затухания:
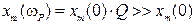 ;
;
11) максимальные значения амплитуды скорости при резонансе.
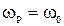 ,
, 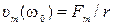 .
.
Сложение колебаний
Сложение колебаний, происходящих вдоль одной оси
1) формулы для определения амплитуды и начальной фазы результирующего колебания:
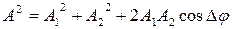 ,
, 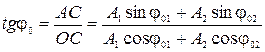 .
.
Биение
2) уравнение биения 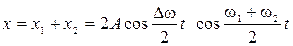 ;
;
3) амплитуда биений  .
.
Сложение взаимно перпендикулярных колебаний
В результате сложения двух взаимно перпендикулярных колебаний с одинаковыми частотами  и
и 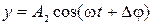 траектория, вдоль которой происходят результирующие колебания, лежит в плоскости ХУ и описывается уравнением:
траектория, вдоль которой происходят результирующие колебания, лежит в плоскости ХУ и описывается уравнением:
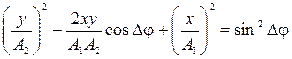 .
.
В случае кратных частот возникают фигуры Лиссажу.
Волны
1) Волна – процесс распространения колебаний в среде:
2) Продольные и поперечные волны. В продольной волне частицы среды совершают колебания вдоль вектора скорости распространения волны, а в поперечной волне - перпендикулярно к нему;
3) Гармоническая (синусоидальная) волна – волна, в которой частицы среды совершают гармонические колебания около своих положений равновесия с определенной циклической частотой 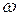 ;
;
4) Период волны (Т) – время одного полного колебания частиц среды.
5) Фазовая скорость волны или скорость распространения волны ( 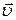 ) – скорость перемещения данной фазы колебаний в среде.
) – скорость перемещения данной фазы колебаний в среде.
6) Длина волны ( 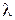 ) – расстояние, которое проходит волна за один период или минимальное расстояние между частицами среды, совершающими колебания с разностью фаз, равной
) – расстояние, которое проходит волна за один период или минимальное расстояние между частицами среды, совершающими колебания с разностью фаз, равной 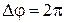 .
. 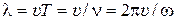 .
.
7) Волновая поверхность – поверхность, проведенная через равновесные положения частиц среды, совершающих колебания в одинаковой фазе. Волновых поверхностей много и они неподвижны.
8) Фронт волны - поверхность, разделяющая частицы среды на вовлеченные и не вовлеченные в колебательное движение. Фронт волны один и он движется со скоростью волны. Можно сказать, что фронт волны это самая дальняя от источника колебаний в данный момент времени волновая поверхность. В каждой точке фронта волны вектор фазовой скорости направлен перпендикулярно к ней.
9) Уравнение плоской волны распространяющейся (волновая функция):
· вдоль оси Ох: 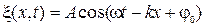
· против оси Ох: 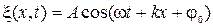
· в произвольном направлении: 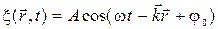
11) Уравнение сферической волны: 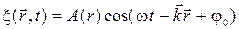
12) Волновой вектор 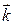 ,модуль волнового вектора
,модуль волнового вектора 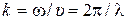
13) Волновые уравнения для плоской гармонической волны, распространяющейся вдоль или против оси Ох

и в произвольном направлении в пространстве:
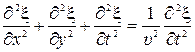
14) Волновое уравнение для сферической волны:
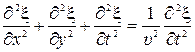
15) Зависимость амплитуды сферической волны от расстояния r до источника колебаний:
А~ 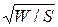 ~
~ 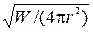 ~
~ 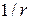 .
.
16) Объемная плотность энергии волны ( 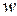 ):
):
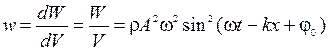
17) Мощность излучения источника колебаний ( 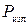 ):
): 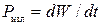
18) Поток энергии 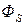 через поверхность (
через поверхность (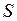 ):
): 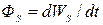
19) Вектор Умова или вектор плотности потока энергии ( 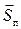 ):
):
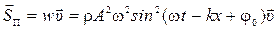
20) Интенсивность упругой волны: 
21) Стоячая волна. Стоячие волны, возникающие при отражении бегущей волны от границы раздела двух сред. Условия образования на границе раздела двух сред узлов и пучностей стоячей волны. Координаты узлов и пучностей стоячей волны:
Узлы 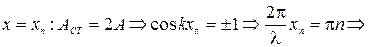
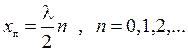
Пучности 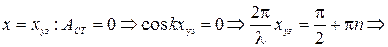
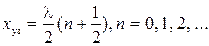
Модуль: Молекулярная физика и термодинамика
Статистический и термодинамический методы описания
макроскопических систем
Основные понятия и определения:
1) Термодинамические (макроскопические) параметры - это величины, которые описывают состояние системы, не рассматривая ее внутреннее строение. К ним относят такие параметры, как температура, давление, объем и т.д.
2) Макросостояние системы – это такое состояние системы, которое определяется заданием ее термодинамических параметров.
3) Микропараметры - это координаты и скорости (импульсы) частиц системы.
4) Микросостояние системы – это состояние системы, определяемое заданием координат и скоростей (импульсов) всех частиц системы.
5) Равновесное состояние системы - такое состояние, при котором ее макропараметры принимают определенное значение и остаются постоянными сколь угодно долго.
Равновесным является такое состояние изолированной системы, в которое она переходит по истечении достаточно большого промежутка времени (в начальный момент времени состояние системы было неравновесным). Это время называют временем релаксации.
6) Идеальный газ – газ, частицы которого на расстоянии не взаимодействуют; а при столкновениях ведут себя как упругие шары; собственный объем частиц значительно меньше объема, занимаемого газом.
7) Функция распределения – плотность вероятности или отношение вероятности 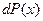 попадания значения случайной величины в отдельном опыте в бесконечно малый интервал значений (
попадания значения случайной величины в отдельном опыте в бесконечно малый интервал значений ( 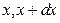 ) к величине этого интервала
) к величине этого интервала
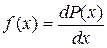 .
.
8) Функция распределения по модулю скорости молекул идеального газа:
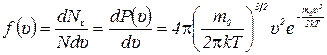 ;
;
9)Относительное число молекул 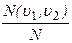 , скорости которых попадают в интервал скоростей (
, скорости которых попадают в интервал скоростей ( 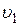 ,
, 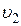 ), или вероятность попадания
), или вероятность попадания 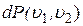 скорости одной молекулы в интервал скоростей (
скорости одной молекулы в интервал скоростей ( 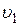 ,
, 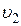 ):
):
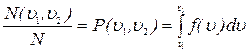 .
.
Основные формулы и соотношения:
10) условие нормировки: 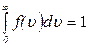 ;
;
11) наиболее вероятная скорость молекул: 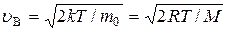 ;
;
12) максимальное значение функции распределения молекул идеального газа по модулю скорости: 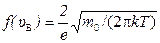 ;
;
13) средняя арифметическая скорость молекул:
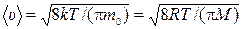
14) средняя квадратичная скорость молекул: < 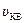 >=
>= 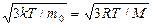
15) средняя кинетическая энергия поступательного движения молекул:
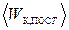
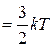
Основное уравнение МКТ идеального газа для давления
1) Уравнение состояния. В связи с тем, что макропараметры системы не являются независимыми, между ними существует вполне определенная формула связи, которая называется уравнением состояния. В самом простом случае, в отсутствие внешних полей (гравитационного, магнитного, электрического полей) такое уравнение связывает такие параметры, как 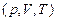
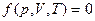 .
.
В более сложных случаях для характеристики равновесного состояния требуются и другие параметры (например, концентрация компонентов смеси газов, напряженность электрического поля, магнитная индукция и т.д.).
Основные формулы и соотношения
2) формулы для давления идеального газа 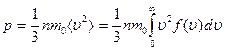 ,
,
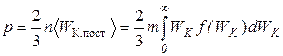 ;
;
3) формула для температуры: 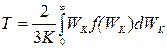 .;
.;
4) нулевое начало термодинамики - в изолированной системе, находящейся в неравновесном состоянии, протекают процессы перехода в равновесное состояние, в котором температура во всех частях системы будет одинаковой.;
5) барометрическая формула: 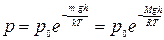 ;
;
6) формулы определения вероятности 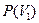 попадания молекулы в произвольный объем
попадания молекулы в произвольный объем 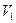 пространства или относительное число молекул
пространства или относительное число молекул 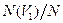 , попадающих в этот объем
, попадающих в этот объем 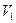 около точки с координатами (
около точки с координатами (  )
)
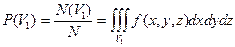 ,
,
7) Формула для экспериментального определения постоянной Авогадро
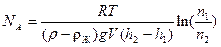 ;
;
8)Уравнение состояния идеального газа:
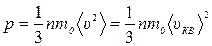 =
= 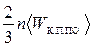
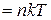 .
.
Расписав концентрацию и введя обозначения: 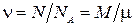 - число молей и
- число молей и 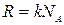 - универсальная газовая постоянная, получим
- универсальная газовая постоянная, получим  ;
;
Термодинамика
Основные понятия и определения:
1) Функция состояния системы это любая функция параметров системы, которая принимает одно и то же значение в данном состоянии системы независимо от способа перехода в это состояние.
2) Неравновесное состояние - состояние, в котором хотя бы один из термодинамических параметров не имеет определенного значения.
11) Процесс релаксации – процесс перехода предоставленной самой себе системы из неравновесного состояния в равновесное состояние.
12) Изолированная (замкнутая) система – система, которая не обменивается с внешними телами энергией и веществом.
13) Закрытая система – система, которая обменивается энергией и не обменивается частицами с окружающими ее внешними телами.
14) Открытая система – система, которая обменивается энергией и частицами с окружающими внешними телами.
15) Равновесный процесс (квазистатический процесс). В равновесной термодинамике изучают равновесные процессы. Под ними понимают процессы, в каждой точке которых макропараметры системы принимают определенные значения. Такие процессы являются идеализацией, они протекают бесконечно медленно в отсутствие разности давлений и температур.
Примером такого процесса является процесс бесконечно медленного сжатия газа под поршнем. В этом случае давление и температура газа будут одинаковыми во всех точках занимаемого газом объема. Если же перемещать поршень с конечной скоростью, то тогда непосредственно под поршнем образуется область газа (воздушная подушка), в которой его давление превышает давление в остальных точках объема. Следовательно, этот параметр для газа будет неопределенным и процесс не будет равновесным.
Равновесные процессы можно изображать на диаграммах состояниях, а неравновесные процессы нельзя из-за неопределенности параметров состояния в каждой точке процесса (их протекание можно обозначить пунктирной линией).
16) Все равновесные процессы являются обратимыми. Равновесный процесс, представляя собой непрерывную цепь равновесных состояний, является обратимым, т.е. обратимый процесс можно совершить в обратном направлении и при этом в окружающей среде не останется никаких изменений.
17) Круговой процесс это процесс, при котором система возвращается в исходное состояние
Внутренняя энергия системы, работа, теплообмен, количество теплоты.
Основные понятия и определения:
1) Внутренняя энергия системы – сумма кинетических энергий теплового движения молекул и потенциальной энергии их взаимодействия: 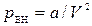 ;
;
2) Числом степеней свободы (  ) называют число независимых между собой возможных перемещений механической системы. число степеней свободы молекулы
) называют число независимых между собой возможных перемещений механической системы. число степеней свободы молекулы
5) Теплообмен (теплопередача) – процесс обмена энергией между системой и внешними телами, при котором не происходит изменение объема системы, не перемещаются ее макроскопические части.
Теплообмен может происходить за счет соударений молекул системы и внешних тел на границе их раздела, за счет лучеиспускания (молекулы системы поглощают электромагнитное излучение внешних источников) и за счет конвекции - процесса переноса тепла в жидкости, газе, сыпучих средах за счет потоков вещества. Примером конвекции является перемешивание нагретых и холодных слоев воздуха в земной атмосфере.
В чистом виде теплообмен реализуется для изохорического процесса ( 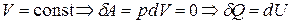 ).
).
6) Количество теплоты (Q) –энергия, получаемая или отдаваемая системой в процессе теплообмена. Если система получает теплоту, то она считается положительной, если отдает - отрицательной.
7) Теплоемкость – количество теплоты, необходимое для изменения температуры системы (тела) на один градус: 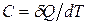 .
.
8) Удельная теплоемкость системы ( 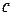 ) :
) : 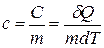 , где
, где 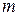 - масса системы
- масса системы
9) Молярная теплоемкость системы ( 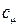 )
) 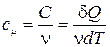 ,
,
10) Формула для количества теплоты: 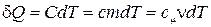 ;
;
Основные формулы и соотношения
11) средняя энергия теплового движения молекулы:
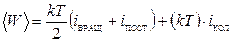
12) элементарная работа: 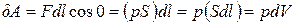 ; работа на конечном перемещении:
; работа на конечном перемещении: 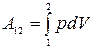 ;
;
13) Первое начало термодинамики: количество теплоты, подведенное к системе, идет на изменение ее внутренней энергии и на работу, совершаемую системой над внешними телами: 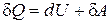 ,
, 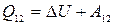 ;
;
14) формула первого начала термодинамики для кругового процесса:
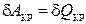 ;
;
Энтропия. Второе начало термодинамики
1) Энтропия – термодинамическая величина, характеризующая меру неупорядоченности (беспорядка) системы,
2) Энтропия функция состояния системы, т.е. она не зависит от пути перехода из одного состояния в другое, а зависит только от начального и конечного состояния системы
3) Уравнение Клаузиуса: 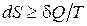 , где знак «=» в случае равновесных процессов, знак «>» – нервановесных.
, где знак «=» в случае равновесных процессов, знак «>» – нервановесных.
Формула для изменения энтропии в равновесном процессе: 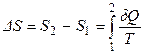 ;
;
4) Второе начало термодинамики – энтропия замкнутой системы стремится может только возрастать или оставаться не низменной: 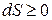 ;
;
5) Статистический смысл энтропии.
Термодинамическая вероятность (статистический вес)( 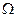 ) -это число микросостояний системы, которые соответствуют данному макросостоянию системы.
) -это число микросостояний системы, которые соответствуют данному макросостоянию системы.
Связь энтропии и термодинамической вероятности: 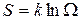 ;
;
7) Третье начало термодинамики – энтропия системы при абсолютном нуле температур равна нулю, т.е. 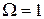 и S=0 при Т=0 К .
и S=0 при Т=0 К .
Применение первого и второго закона термодинамики.
к изопроцессам в идеальном газе.
1) Изотермический процесс ( 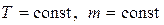 ).
).
· Уравнение процесса: 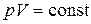 .
.
· 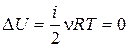 ,
,
· 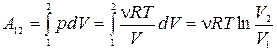 ,
,
· 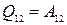 ,
,
· 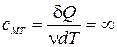 ,
,
· 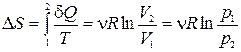 .
.
Отметим, что молярная теплоемкость при этом процессе равна бесконечности, так как любой подвод тепла идет на совершение газом работы и при этом температура системы не изменяется.
2) Изохорический процесс( 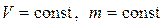 ).
).
· Уравнение процесса: 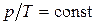 .
.
· 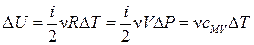 ,
,
· 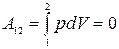 ,
, 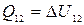 ,
,
· 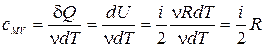 ,
,
· 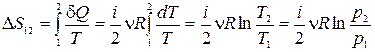 .
.
3) Изобарический процесс( 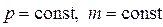 ).
).
· Уравнение процесса: 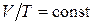 .
.
· 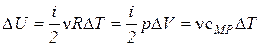 ,
,
· 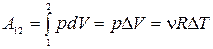 ,
,
· 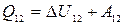 ,
,
· 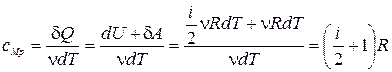 ,
,
·  .
.
Отметим, что разность теплоемкостей 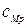 и
и 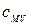 для идеального газа равна
для идеального газа равна
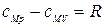 .
.
Это уравнение получило название уравнения Майера.
4) Адиабатический процесс(изоэнтропийный процесс,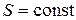 ) – это процесс, происходящий в системе без теплообмена (Q=0) с внешними телами, или это изоэнтропийный процесс, при его протекании энтропия системы не изменяется.
) – это процесс, происходящий в системе без теплообмена (Q=0) с внешними телами, или это изоэнтропийный процесс, при его протекании энтропия системы не изменяется.
· Уравнения адиабатического процесса:
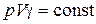 или
или 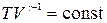 или
или 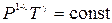 ,
,
где 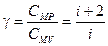 – коэффициент Пуассона;
– коэффициент Пуассона;
· 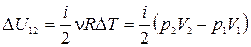 ,
,
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|