Производные и дифференциалы высших порядков

22.7. Производные и дифференциалы высших порядков

Определение 22.1.

Второй производной (или производной второго порядка) функции 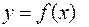называется производная от ее первой производной.

Обозначение: 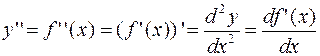(22.6)

Механический смысл.

Функция 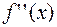равна ускорению движущейся точки в момент времени .

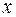Аналогично определяются 3-я, 4-я и т.д. производные:

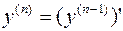(22.7)

а). Если 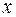- независимая переменная, то 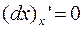, т.к. 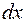не зависит от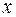

Определение 22.2.

Вторым дифференциалом от функции 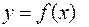называется дифференциал от первого дифференциала:

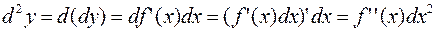(22.8)

Тогда 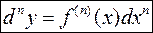(22.9)

– формула n-го дифференциала функции .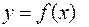

б). Если 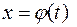, то есть 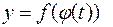, тогда, поскольку 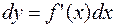, то

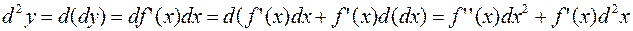Здесь (**).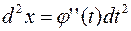

Замечание 2. 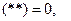если .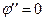

Таким образом, свойство инвариантности не выполняется.