Графический метод решения неравенств

Графический метод решения неравенств

Построение графиков значительно упрощает решение уравнений, содержащих параметр. Использование графического метода при решении неравенств с параметром еще нагляднее и целесообразнее.

Графическое решение неравенств вида f(x) ≥ g(x) означает нахождение значений переменной х, при которых график функции f(x) лежит выше графика функции g(x). Для этого всегда необходимо найти точки пересечения графиков (если они существуют).

Пример 1.

Решить неравенство |x + 5| < bx.

Решение.

Строим графики функций у = |x + 5| и у = bx (рис. 2). Решением неравенства будут те значения переменной х, при которых график функции у = |x + 5| будет находиться ниже графика функции у = bx.

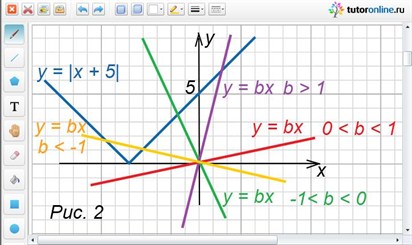
На рисунке видно:

1) При b > 1 прямые пересекаются. Абсцисса точки пересечения графиков этих функций есть решение уравнения х + 5 = bx, откуда х = 5/(b – 1). График у = bx находится выше при х из интервала (5/(b – 1); +∞), значит это множество и есть решение неравенства.

2) Аналогично находим, что при -1 < b < 0 решением является х из интервала (-5/(b + 1); 5/(b – 1)).

3) При b ≤ -1 x ? (-∞; 5/(b – 1)).

4) При 0 ≤ b ≤ 1 графики не пересекаются, а значит, и решений у неравенства нет.

Ответ: x ? (-∞; 5/(b – 1)) при b ≤ -1;
x ? (-5/(b + 1); 5/(b – 1)) при -1 < b < 0;
решений нет при 0 ≤ b ≤ 1; x ? (5/(b – 1); +∞) при b > 1.

Пример 2.

Решить неравенство а(а + 1)х > (a + 1)(a + 4).

Решение.

1) Найдем «контрольные » значения для параметра а: а₁ = 0, а₂ = -1.

2) Решим данное неравенство на каждом подмножестве действительных чисел: (-∞; -1); {-1}; (-1; 0); {0}; (0; +∞).

a) a < -1, из данного неравенства следует, что х > (a + 4)/a;

b) a = -1, тогда данное неравенство примет вид 0·х > 0 – решений нет;

c) -1 < a < 0, из данного неравенства следует, что х < (a + 4)/a;

d) a = 0, тогда данное неравенство имеет вид 0 · х > 4 – решений нет;

e) a > 0, из данного неравенства следует, что х > (a + 4)/a.

⇐ Предыдущая 123 Следующая ⇒