
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Дифференциальные уравнения второго порядка
§ 2. Дифференциальные уравнения второго порядка
Линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами 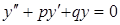 имеет общее решение
имеет общее решение 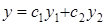 , где
, где 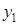 и
и 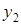 линейно-независимые частные решения этого уравнения.
линейно-независимые частные решения этого уравнения.
Общий вид решений однородного дифференциального уравнения второго порядка с постоянными коэффициентами 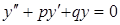 , зависит от корней характеристического уравнения
, зависит от корней характеристического уравнения  .
.
| Корни характеристического уравнения | Вид общего решения |
Корни 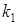 и и 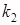 действительные и различные действительные и различные
| 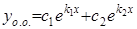
|
Корни 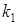 = = 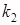 = = 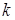 действительные и одинаковые
действительные и одинаковые
| 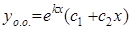
|
Корни комплексные 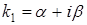 , , 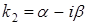
| 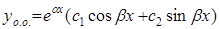
|
Пример
Найти общее решение линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами:
1) 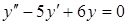
Решение: Составим характеристическое уравнение: 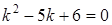 .
.
Решив его, найдем корни 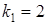 ,
, 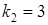 действительные и различные. Следовательно, общее решение имеет вид:
действительные и различные. Следовательно, общее решение имеет вид: 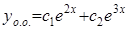 .
.
2) 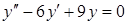
Решение: Составим характеристическое уравнение: 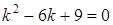 .
.
Решив его, найдем корни 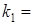
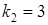 действительные и одинаковые. Следовательно, общее решение имеет вид:
действительные и одинаковые. Следовательно, общее решение имеет вид: 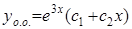 .
.
3) 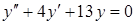
Решение: Составим характеристическое уравнение: 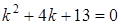 .
.
Решив его, найдем корни 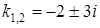 комплексные. Следовательно, общее решение имеет вид:
комплексные. Следовательно, общее решение имеет вид: 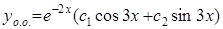 .
.
Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиимеет вид
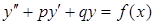 , где
, где 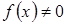 . (1)
. (1)
Общее решение линейного неоднородного дифференциального уравнения второго порядка 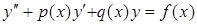 имеет вид
имеет вид 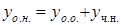 , где
, где 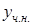 – частное решение этого уравнения,
– частное решение этого уравнения, 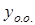 – общее решение соответствующего однородного уравнения, т.е. уравнения
– общее решение соответствующего однородного уравнения, т.е. уравнения 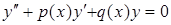 .
.
Вид частного решения 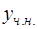 неоднородного уравнения (1) в зависимости от правой части
неоднородного уравнения (1) в зависимости от правой части 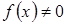 :
:
Правая часть 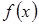
| Частное решение 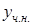
|
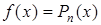 – многочлен степени – многочлен степени 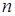
| 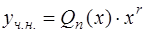 , где , где 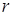 – число корней характеристического уравнения, равных нулю. – число корней характеристического уравнения, равных нулю.
|
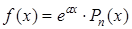
|  , где , где 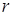 – число, показывающее, сколько раз – число, показывающее, сколько раз 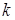 = =  является корнем характеристического уравнения. является корнем характеристического уравнения.
|
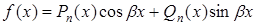
| 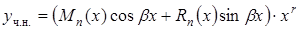 , где , где 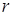 – число, равное числу корней характеристического уравнения, совпадающих с – число, равное числу корней характеристического уравнения, совпадающих с 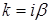 . .
|
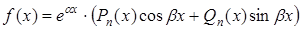
| 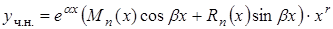 где где 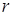 – число корней характеристического уравнения, совпадающих с – число корней характеристического уравнения, совпадающих с 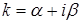 . .
|
Рассмотрим различные виды правых частей линейного неоднородного дифференциального уравнения 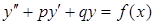 :
:
1. Пусть правая часть имеет вид 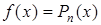 , где
, где 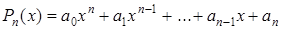 – многочлен степени
– многочлен степени 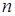 . Тогда частное решение
. Тогда частное решение 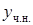 можно искать в виде
можно искать в виде 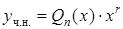 , где
, где  – многочлен той же степени, что и
– многочлен той же степени, что и 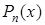 , а
, а 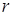 – число корней характеристического уравнения, равных нулю.
– число корней характеристического уравнения, равных нулю.
Пример
Найти общее решение 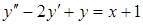 .
.
Решение:
А) Найдем общее решение соответствующего однородного уравнения 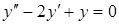 . Для этого запишем характеристическое уравнение
. Для этого запишем характеристическое уравнение 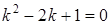 . Найдем корни последнего уравнения
. Найдем корни последнего уравнения 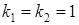 . Следовательно, общее решение однородного уравнения имеет вид
. Следовательно, общее решение однородного уравнения имеет вид 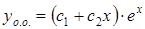 .
.
Б) Так как правая часть уравнения является многочленом первой степени и ни один из корней характеристического уравнения 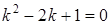 не равен нулю (
не равен нулю ( 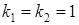 ), то частное решение ищем в виде
), то частное решение ищем в виде 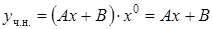 , где
, где 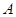 и
и 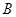 – неизвестные коэффициенты. Дифференцируя дважды
– неизвестные коэффициенты. Дифференцируя дважды 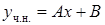 и подставляя
и подставляя 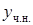 ,
, 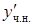 и
и 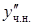 в исходное уравнение, находим
в исходное уравнение, находим 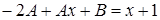 .
.
Приравнивая коэффициенты при одинаковых степенях 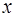 в обеих частях равенства
в обеих частях равенства 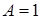 ,
, 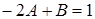 , находим
, находим 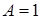 ,
, 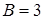 . Итак, частное решение данного уравнения имеет вид
. Итак, частное решение данного уравнения имеет вид 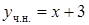 , а его общее решение
, а его общее решение 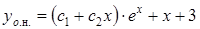 .
.
2. Пусть правая часть имеет вид 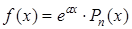 , где
, где 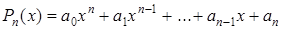 – многочлен степени
– многочлен степени 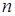 . Тогда частное решение
. Тогда частное решение 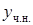 можно искать в виде
можно искать в виде  , где
, где  – многочлен той же степени, что и
– многочлен той же степени, что и 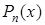 , а
, а 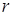 – число, показывающее, сколько раз
– число, показывающее, сколько раз 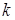 является корнем характеристического уравнения.
является корнем характеристического уравнения.
Пример
Найти общее решение 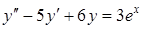 .
.
Решение:
А) Найдем общее решение соответствующего однородного уравнения 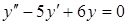 . Для этого запишем характеристическое уравнение
. Для этого запишем характеристическое уравнение 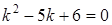 . Найдем корни последнего уравнения
. Найдем корни последнего уравнения 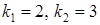 . Следовательно, общее решение однородного уравнения имеет вид
. Следовательно, общее решение однородного уравнения имеет вид 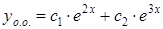 .
.
Б) Так как правая часть уравнения есть функция 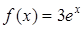 , то контрольное число данного уравнения
, то контрольное число данного уравнения 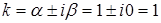 , оно не совпадает с корнями
, оно не совпадает с корнями 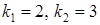 характеристического уравнения
характеристического уравнения 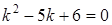 . Тогда частное решение ищем в виде
. Тогда частное решение ищем в виде 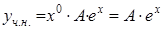 , где
, где 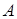 – неизвестный коэффициент. Дифференцируя дважды
– неизвестный коэффициент. Дифференцируя дважды 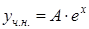 и подставляя
и подставляя 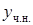 ,
, 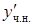 и
и 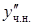 в исходное уравнение, находим
в исходное уравнение, находим 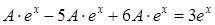 . Откуда
. Откуда 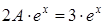 , то есть
, то есть 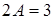 или
или 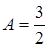 .
.
Итак, частное решение данного уравнения имеет вид 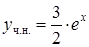 , а его общее решение
, а его общее решение 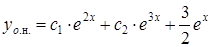 .
.
3. Пусть правая часть имеет вид 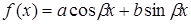 , где
, где 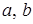 и
и 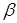 – данные числа. Тогда частное решение
– данные числа. Тогда частное решение 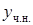 можно искать в виде
можно искать в виде 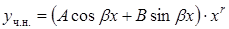 , где
, где 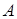 и
и 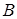 – неизвестные коэффициенты, а
– неизвестные коэффициенты, а 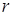 – число, равное числу корней характеристического уравнения, совпадающих с
– число, равное числу корней характеристического уравнения, совпадающих с 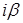 . Если в выражение функции
. Если в выражение функции 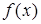 входит хотя бы одна из функций
входит хотя бы одна из функций 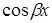 или
или 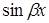 , то в
, то в 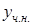 надо всегда вводить обе функции.
надо всегда вводить обе функции.
Пример
Найти общее решение 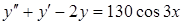 .
.
Решение:
А) Найдем общее решение соответствующего однородного уравнения 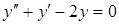 . Для этого запишем характеристическое уравнение
. Для этого запишем характеристическое уравнение 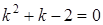 . Найдем корни последнего уравнения
. Найдем корни последнего уравнения 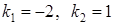 . Следовательно, общее решение однородного уравнения имеет вид
. Следовательно, общее решение однородного уравнения имеет вид 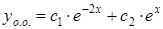 .
.
Б) Так как правая часть уравнения есть функция 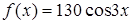 , то контрольное число данного уравнения
, то контрольное число данного уравнения 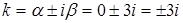 , оно не совпадает с корнями
, оно не совпадает с корнями 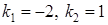 характеристического уравнения
характеристического уравнения 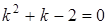 . Тогда частное решение ищем в виде
. Тогда частное решение ищем в виде
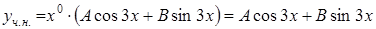 , где
, где 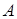 и
и 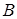 – неизвестные коэффициенты. Дифференцируя дважды
– неизвестные коэффициенты. Дифференцируя дважды 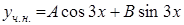 , получим
, получим 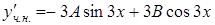 и
и 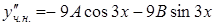 . Подставляя
. Подставляя 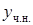 ,
, 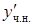 и
и 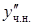 в исходное уравнение, находим
в исходное уравнение, находим
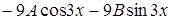
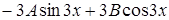
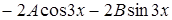
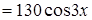 .
.
Приводя подобные слагаемые, получим
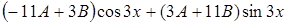
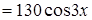 .
.
Приравниваем коэффициенты при 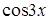 и
и 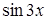 в правой и левой частях уравнения соответственно. Получаем систему
в правой и левой частях уравнения соответственно. Получаем систему 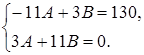 . Решая ее, находим
. Решая ее, находим 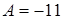 ,
, 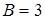 .
.
Итак, частное решение исходного дифференциального уравнения имеет вид 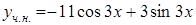 .
.
Общее решение исходного дифференциального уравнения имеет вид
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|