Дифференциальные уравнения первого порядка

§ 1. Дифференциальные уравнения первого порядка

1. Дифференциальные уравнения с разделяющимися переменными имеют вид .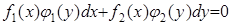

Если ни одна из функций не равна тождественно нулю, то в результате деления исходного уравнения на 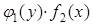оно приводится к виду .

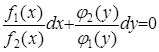Почленное интегрирование приводит к соотношению 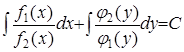, которое и определяет (в неявной форме) решение исходного уравнения. Решение дифференциального уравнения, выраженное в неявной форме, называют общим интегралом этого уравнения.

Пример

Найти частное решение дифференциального уравнения 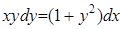, удовлетворяющее начальному условию .

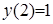Решение:

Данное уравнение является уравнением с разделяющимися переменными. Разделим обе части уравнения на функци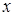и и 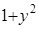. Получим 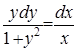. Проинтегрируем это равенство: 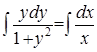, получим .

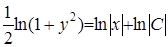Здесь в качестве произвольной постоянной взяли 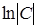(С = const).

Общее решение уравнения можно записать в виде .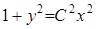

Выделим из полученного общего решения частное решение, исходя из начального условия 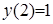. Подставляя эти значения в общее решение, получаем 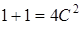или 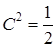. Следовательно, частное решение задается уравнением 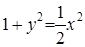или .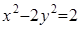

Последнее уравнение задает на плоскости 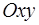гиперболу. Нетрудно убедиться, что общее решение данного дифференциального уравнения задает семейство гипербол.

12 3 Следующая ⇒