Контакты

Случайная статья

Линейные дифференциальные уравнения первого порядка. Уравнения Бернулли

⇐ ПредыдущаяСтр 2 из 3Следующая ⇒

2. Линейные дифференциальные уравнения первого порядка. Уравнения Бернулли

Уравнение вида 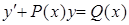называется линейным ( и 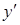входят в первых степенях, не перемножаясь между собой).

Если , то уравнение называется линейным неоднородным.

Если 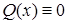, то уравнение называется линейным однородным (д. у. с разделяющимися переменными).

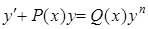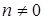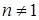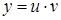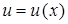Уравнение (нелинейное) вида , где , называется уравнением Бернулли. Данные уравнения можно интегрировать методом Бернулли, т.е. с помощью подстановки , где , – неизвестные функции.

Пример

Найти частное решение дифференциального уравнения 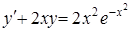, удовлетворяющее начальным условиям .

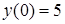Решение: Это линейное неоднородное дифференциальное уравнение.

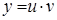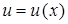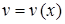Полагаем , где , - неизвестные функции, 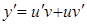. Подставляя 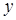и 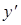в исходное уравнение, имеем .

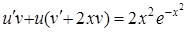1) Подберем функцию 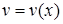так, чтобы выражение, содержащееся в скобках, обращалось в нуль, т.е. 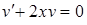, откуда 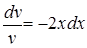. После интегрирования получаем 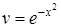(постоянную интегрирования берем равной нулю).

2) Для определения функции имеем 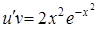или 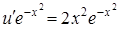, т.е. 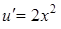, откуда .

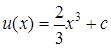3) Таким образом, общее решение исходного уравнения имеет вид

.

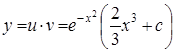4) Используя начальное условие, вычисляем значение постоянной :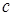

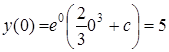, т.е. .

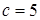Поэтому частное решение исходного дифференциального уравнения, удовлетворяющее заданному начальному условию, имеет вид

.

⇐ Предыдущая 123 Следующая ⇒

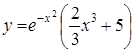© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.