Теорема 1. Математическое ожидание случайной величины, распределённой по биноминальному закону с параметрами n и p, равно произведению np, то есть

Решение.

Для того чтобы проверить задан ли закон распределения нужно найти сумму чисел записанных в таблице во второй строке. Если сумма равна 1, то закон распределения задан. Если сумма не равна 1, то закон распределения не задан.

а) 0,1+0,15+0,1+0,3+0,15+0,2=1.

Значит, первая таблица задает закон распределения дискретной случайной величины.

б) 0,1+0,15+0,2+0,15+0,1+0,1+0,3=1,1.

Значит, вторая таблица не задает закон распределения дискретной случайной величины.

Определение:Математическим ожиданиемслучайной величины называется число, равное сумме произведений всех значений случайной величины на вероятности этих значений.

Математическое ожидание случайной величины Xобозначается через MX. Если случайная величина X принимает значения 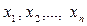соответственно с вероятностями 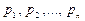, то согласно определению:

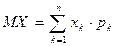. (1)

Математическое ожидание часто называют средним значением случайной величины, так как оно указывает некоторое «среднее число», около которого группируются все значения случайной величины.

Определение: Пусть задан закон распределения случайной величины X:

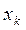
			…	k	…	n
			…		…

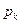
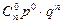
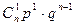
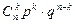
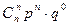
Тогда такое распределение называется распределением Я. Бернуллиили биноминальным распределением, причём верно равенство

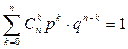. (2)

Теорема 1. Математическое ожидание случайной величины, распределённой по биноминальному закону с параметрами n и p, равно произведению np, то есть

⇐ Предыдущая 123 4 Следующая ⇒