Практическое занятие № 10.. Тема: «Решение простейших задач теории вероятностей и математической статистики». Теоретическая часть. Пример 2.

Практическое занятие № 10.

Тема: «Решение простейших задач теории вероятностей и математической статистики»

Цель работы:

Закрепить навыки построения закона распределения дискретной случайной величины по заданному условию.

Теоретическая часть

Случайная величина – величина, численное значение которой может меняться в зависимости от результата стохастического эксперимента.

Дискретной назовём случайную величину, возможные значения которой образуют конечное множество.

Законом распределения дискретной случайной величины называется правило, по которому каждому возможному значению x_i ставится в соответствие вероятность p_i, с которой случайная величина может принять это значение, причём .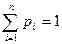

Пример 1.Абитуриент сдаёт два вступительных экзамена: по математике и физике. Составить закон распределения случайной величины х, числа полученных пятёрок, если вероятность получения пятёрки по математике равна 0,8, а по физике – 0,6.

Решение.Обозначим А₁ и А₂– события, заключающиеся в том, что и математика, и физика сданы на 5. Очевидно, возможные значения х есть 0, 1, 2, причём

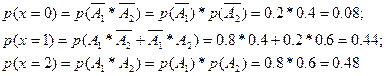
Полученные результаты сведём в таблицу:

x_i
p_i	0.08	0.44	0.48

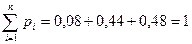Пример 2.

Задают ли законы распределения дискретной случайной величины следующие таблицы?

а)

х
р	0,1	0,15	0,1	0,3	0,15	0,2

б)

х
р	0,1	0,15	0,2	0,15	0,1	0,1	0,3

12 3 4 Следующая ⇒