Сочетания. Порядок не важен!. Свойства вероятности.

3. Сочетания

Сочетаниями из n элементов по m элементов 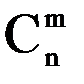называются комбинации из n элементов по m элементов, которые отличаются друг от друга только составом элементов.

! Порядок не важен!

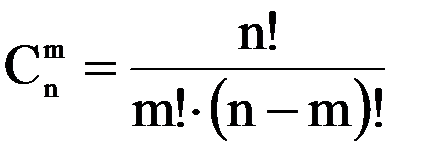
Пример 6.Вычислить число сочетаний из 9 по 4.

Решение.

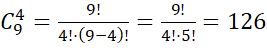
Пример 7.В первенстве по шахматам участвует 20 человек, а в финал выходят лишь трое. Сколькими способами можно определить эту тройку?

Решение. В данном случае порядок, в котором располагается эта тройка, не важен. Поэтому тройки, вышедшие в финал – это сочетания из 20 по 3.

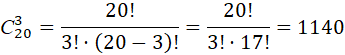
Классическое определение вероятности.

Определение.Пусть для того, чтобы выяснить, произойдет или не произойдет событие А нужно произвести испытание. Будем считать, что все исходы этого испытания попарно несовместны и равновозможны и их количество равно n. Среди этих n исходов выделим те, которые благоприятны для события А, т. е. те, при которых событие А происходит. Пусть количество благоприятных для события А исходов равно m. Тогда вероятностью события А называется отношение числа благоприятных исходов к числу всех исходов испытания, то есть

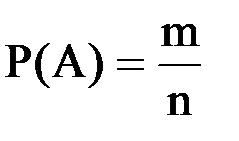
Свойства вероятности.

1⁰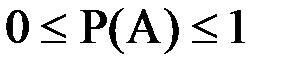

2⁰ Вероятность достоверного события равна 1

3⁰ Вероятность невозможного события равна 0

⇐ Предыдущая 123 Следующая ⇒