Реализация в R

Реализация в R

В R множественные сравнения групповых средних при помощи теста Тьюки можно выполнить несколькими способами. В этом сообщении мы рассмотрим функцию TukeyHSD(), входящую в базовую версию R.

В качестве примера используем данные по содержанию стронция (мг/мл) в пяти водоемах США (пример заимствован из книги Zar 1999):

waterbodies <- data.frame(Water = rep(c("Grayson", "Beaver",

"Angler", "Appletree",

"Rock"), each = 6),

Sr = c(28.2, 33.2, 36.4, 34.6, 29.1, 31.0,

39.6, 40.8, 37.9, 37.1, 43.6, 42.4,

46.3, 42.1, 43.5, 48.8, 43.7, 40.1,

41.0, 44.1, 46.4, 40.2, 38.6, 36.3,

56.3, 54.1, 59.4, 62.7, 60.0, 57.3)

)

На рисунке ниже эти данные представлены графически:

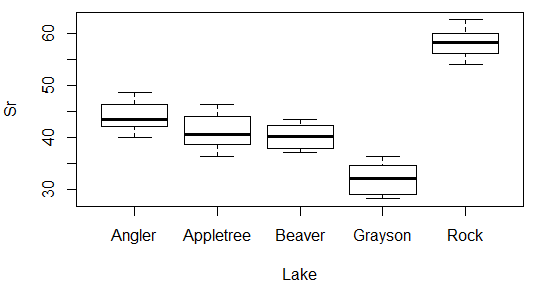
Необходимо выяснить, 1) есть ли существенные различия между этими водоёмами по содержанию стронция в целом и, если есть, 2) какие именно водоемы отличаются друг от друга. Для ответа на первый вопрос выполним дисперсионный анализ при помощи функции aov():

M <- aov(Sr ~ Water, data = waterbodies)

summary(M)

Df Sum Sq Mean Sq F value Pr(>F)

Water 4 2193.4 548.4 56.16 3.95e-12 ***

Residuals 25 244.1 9.8

---

Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Как видно из полученных результатов, обследованные водоемы статистически значимо различаются по содержанию стронция. Для того чтобы выяснить, где именно лежат различия, достаточно подать объект M на функцию TukeyHSD():

TukeyHSD(M)

Tukey multiple comparisons of means

95% family-wise confidence level

Fit: aov(formula = Sr ~ Water, data = waterbodies)

$Water

diff lwr upr p adj

Appletree-Angler -2.9833333 -8.281979 2.315312 0.4791100

Beaver-Angler -3.8500000 -9.148645 1.448645 0.2376217

Grayson-Angler -12.0000000 -17.298645 -6.701355 0.0000053

Rock-Angler 14.2166667 8.918021 19.515312 0.0000003

Beaver-Appletree -0.8666667 -6.165312 4.431979 0.9884803

Grayson-Appletree -9.0166667 -14.315312 -3.718021 0.0003339

Rock-Appletree 17.2000000 11.901355 22.498645 0.0000000

Grayson-Beaver -8.1500000 -13.448645 -2.851355 0.0011293

Rock-Beaver 18.0666667 12.768021 23.365312 0.0000000

Rock-Grayson 26.2166667 20.918021 31.515312 0.0000000

В первом столбце полученной таблицы перечислены пары сравниваемых водоемов. Во втором столбце содержатся разности между соответствующими групповыми средними. Третий и четвертый столбцы содержат значения нижнего (lwr) и верхнего (upr) 95%-ных доверительных пределов для соответствующих разностей. Наконец, в пятом столбце представлены Р-значения для каждой из сравниваемых пар водоемов. Хорошо видно, что существенной разницы в парах "Appletree-Angler", "Beaver-Angler" и "Beaver-Appletree" нет (Р > 0.05), тогда как во всех остальных случаях разница статистически значима. В целом полученные результаты хорошо согласуются визуальной оценкой различий, которую можно сделать, глядя на приведенную выше диаграмму размахов.

Результаты попарных сравнений групповых средних можно легко изобразить на графике:

par(mar = c(4.5, 8, 4.5, 4.5))

plot(TukeyHSD(M), las = 1)

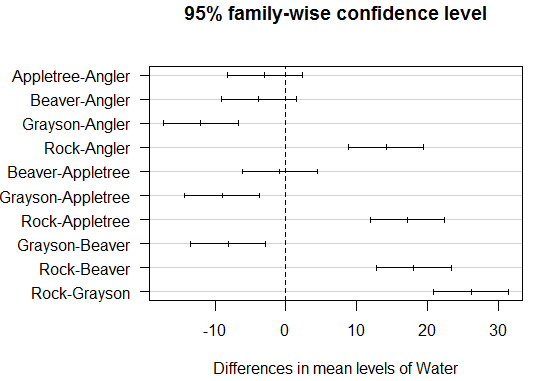
На представленном рисунке приведены разности между групповыми средними (Differences in mean levels of Water) и их доверительные интервалы, рассчитанные с учетом контроля над групповой вероятностью ошибки (95% family-wise confidence level). В трех случаях доверительные интервалы включают 0, что указывает на отсутствие различий между соответствующими группами (сравните с Р-значениями выше).

Условия применимости критерия Тьюки

Хотя теория того не требует, критерий Тьюки и другие подобные ему методы рекомендуется применять после того, как дисперсионный анализ установил наличие существенной разницы между группами в целом (Zar 1999). В связи с этим критерий Тьюки относится к методам апостериорного анализа (post-hoc analysis).

Критерий Тьюки имеет те же условия применимости, что и собственно дисперсионный анализ, т.е. нормальность распределения данных и (особенно важно!) однородность групповых дисперсий (подробнее см. здесь). Устойчивость к отклонению от этих условий, равно как и статистическая мощность критерия Тьюки, возрастают при одинаковом числе наблюдений во всех сравниваемых группах (Zar 1999).

критерий Тьюкимножественные сравнения

⇐ Предыдущая 1 234 Следующая ⇒