Комбинированные системы рычаги + блоки

Комбинированные системы рычаги + блоки

9.Вверх или вниз будет двигаться груз весом 1 Н? Какой груз надо подвесить вместо него, чтобы система находилась в равновесии?

Ответ: вверх, 8/3Н

10. 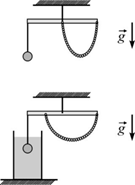Однородная линейка подвешена к потолку на нити, привязанной к середине линейки. К линейке прикреплены груз и однородная цепочка так, как показано на первом рисунке. При этом линейка горизонтальна и находится в равновесии. Затем груз полностью погрузили в воду так, что он не касался дна и стенок стакана. Для того, чтобы сохранить равновесие системы, пришлось переместить точку прикрепления к линейке одного из концов цепочки на 1/4 длины линейки – как показано на втором рисунке. Какова средняя плотность материала, из которого сделан груз?

Ответ: плотность груза равна ρ_груз = 2ρ_воды = 2000кг/м³.

Из условия равновесия линейки в исходном положении найдена связь массы груза с массой цепочки – 2 очка. Записана связь плотности и объема груза с массой цепочки – 2 очка. Записано (или использовано) уравнение моментов (условие равновесия линейки) в конечном положении – 4 очка. Найдена плотность груза – 2 очка.

11. Через неподвижный блок перекинута легкая нерастяжимая нить, на которой висят два стальных цилиндрических бруска. Масса левого бруска m₁= 1кг. Вначале к нижнему основанию правого бруска был приморожен кусок льда неизвестной массы, а сами бруски удерживались вручную. Правый брусок с примороженным к нему куском льда погрузили в воду комнатной температуры, налитую в очень широкий сосуд, после чего бруски отпустили. Сразу после этого оказалось, что система находится в равновесии, когда правый брусок погружен в воду наполовину своей высоты. После того, как весь лед растаял, правый брусок полностью погрузился в воду. При этом система снова оказалась в равновесии. Найдите массу правого бруска, а также массу примороженного к нему льда. Плотность воды 1000кг/м³, льда 900 кг/м³, плотность стали 7800 кг/м³. Изменением уровня воды в сосуде пренебречь.

Ответ: m₂= m₁ρ_c/(ρ_c – ρ_в) ≈1,15кг; m_л= m₁ρ_в ρ_л /(ρ_c – ρ_в) (ρ_в– ρ_л) ≈0,66кг

12. 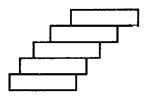Пять кирпичей длиной l кладут без раствора один на другой так, что каждый кирпич выступает над нижележащим (см. рисунок). На какое наибольшее расстояние правый край самого верхнего кирпича может выступать над правым краем самого нижнего кирпича?

Решение.Первый кирпич может выступать над краем второго не более, чем на L/2. Тогда общий центр тяжести С₂ двух верхних кирпичей расположен на расстоянии L/4 по горизонтали от края второго кирпича. Именно на это расстояние и может выступать второй кирпич над третьим. Центр тяжести трех верхних кирпичей С₃ определяется из условия mg(L/2-x) = 2mgx, откуда x=L/6, т.е. третий кирпич может выступать над четвертым на 1/6 своей длины. Аналогично доказывается, что четвертый кирпич может выступать над пятым на 1/8 своей длины. Полное смещение верхнего кирпича относительно нижнего составит L/2+L/4+L/6+L/8=25L/24. Верхний кирпич может целиком выйти за пределы площади опоры!

Ответ: 25L/24

Домашнее задание

13.Два груза с массами m₁=100г и m₂=200г уравновешены на неравноплечих весах. Грузы меняют местами, добавляя к грузу m₂ точно такой же груз, и равновесие весов нарушается. Какой дополнительный груз следует добавить к грузу m₁, чтобы равновесие весов восстановилось?

Решение. Условия равновесия грузов в первом и втором случае дают m₁L₁ = m₂L₂2m₂L₁ = (m₁ + ∆m)L₂, где L_l и L₂ - плечи весов, ∆m - масса дополнительного груза. Деля уравнения друг на друга, находим ∆m = (2m₂²- m₁²)/m₁=700г

⇐ Предыдущая 1 2 345 Следующая ⇒