Простые рычаги

Олимпиадная подготовка по теме «Статика»

Простые рычаги

1.Однажды я подстрелил удивительно большого гуся (дикого!) и множество обычных (совершенно одинаковых!) куропаток. Меня заинтересовало, во сколько раз гусь тяжелее куропатки. По моей просьбе слуга вырезал ровную палку и, привязав к ней веревку, сделал рычажные весы. Сначала я подвесил гуся слева; чтобы уравновесить его, справа пришлось подвесить связку из 40 куропаток. Однако когда я подвесил гуся справа, то, к моему удивлению, для уравновешивания хватило всего 10 куропаток! Я, конечно, тут же сообразил, что мой слуга сделал весы неравноплечими. Более того, я сразу определил, во сколько раз гусь на самом деле тяжелее куропатки, да к тому же — во сколько раз одно плечо самодельных весов длиннее другого. Попробуйте сделать это и вы (чтобы не затруднять вас слишком, разрешаю массой палки пренебречь).

Решение:Пусть вес гуся Р_г,вес куропатки Р_к, а длины левого и правого плеча самодельных весов L_ли L_п. Условие равновесия в двух взвешиваниях: Р_г L_л= 40Р_к L_пи Р_г L_п= 10Р_к L_л. Обозначим отношения Р_г /Р_к = x; L_л/ L_п= y, получим систему уравнений:

xy = 40; x/y = 10. Отсюда легко находим х = 20; y = 2. Это означает, что гусь в 20 раз тяжелее куропатки, а левое плечо вдвое длиннее правого. Т.о. истинный вес гуся равен не среднему арифметическому результатов двух взвешиваний Р_г = (40+10)/2 Р_к =25 Р_к, а их среднему геометрическому: Р_г =√40∙10 Р_к =20 Р_к.

Ответ:гусь в 20 раз тяжелее куропатки, левое плечо вдвое длиннее правого

2.«Хитрый» продавец на рынке торгует рыбой, взвешивая её на весах, сделанных из палки и верёвки (см. рисунок), причём не обманывает покупателей. Покупателю разрешается взвесить рыбу самому, но при условии, что рыба помещается только на левую чашку весов и не снимается до момента расплаты. Продавец разрешает провести максимум два взвешивания, предоставляя покупателю набор гирь. Как определить массу понравившейся вам рыбы? «Коромысло» весов с пустыми чашками занимает горизонтальное положение.

РешениеИз рисунка (в условии задачи) понятно, что продавец использует неравноплечие весы, причём длины плеч весов неизвестны и по условию задачи измерять их нельзя! Сначала, ради интереса, рассмотрим, как взвешивает рыбу продавец. Он может взвесить рыбу сначала на одной чашке весов, уравновесив её гирями массой m₁, а затем на второй чашке, уравновесив её гирями массой m₂. Обозначим длину одного из плеч весов 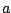, а другого 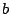. Тогда условия равновесия весов при первом и втором взвешиваниях запишутся в виде: ma = m₁b, m₂a = mb,
где m — неизвестная масса рыбы. Разделив эти соотношения друг на друга, получим: m²= m₁m₂ , откуда m= √m₁m₂ .

Покупателю этот путь недоступен, так как рыба всё время лежит на одной чашке весов. Однако, он может взвесить рыбу сначала на одной чашке весов, уравновесив её гирями массой m₁, а затем может добавить на чашку, где лежит рыба, гирю известной массы m₃, и вновь провести взвешивание. При этом чашка с рыбой и гирей будет уравновешена гирями массой m₄. Условия равновесия весов в этом случае запишутся в виде:

ma = m₁b, (m+m₃)a = m₄b
Разделив эти соотношения друг на друга, получим: m/(m+m₃) = m₁/m₄, откуда для истинной величины массы рыбы 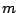получается следующее выражение: m = m₁m₃/(m₄- m₁)

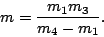Так как в знаменателе стоит разность масс гирь при двух взвешиваниях, то для повышения точности измерений необходимо, чтобы эта разность была не очень мала, то есть нужно, чтобы массы m₁ и m₄ были не очень близки. Этого можно достичь, выбирая гирю m₃ побольше, тогда полученный результат будет точнее. Ответ

12 3 4 5 Следующая ⇒