Массивный рычаг

Массивный рычаг

3. Конец однородного стержня длиной 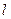согнули под прямым углом так, что длина согнутого участка составляет четвертую часть длины стержня. На каком расстоянии 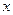от согнутого конца нужно расположить точечную опору, чтобы стержень находился в равновесии?

Решение: Условие равновесия стержня дает mx/4 + mx²/2L = m[(n-1)L/n – x]²/2L, где 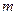- масса стержня. Отсюда находим x = 9L/32 (решение через центр тяжести несогнутой части проще и приводит к тому же ответу).

4.Чтобы узнать массу линейки, на один из ее концов положили груз массой 250 г и начали выдвигать этот конец за край стола. Линейка находилась в равновесии до тех пор, пока ее не выдвинули на четверть длины. Чему равна масса линейки? Насколько можно было бы выдвинуть линейку, если бы масса груза была 125 г?

Ответ: 250г; 1/3 линейки

5.Груз неизвестной массы взвешивают, уравновешивая его гирей с известной массой

M = 6кг на концах тяжёлого прямого коромысла; при этом равновесие достигается, когда точка опоры коромысла смещается от его середины на х=1/4 его длины в сторону гирьки. В отсутствие же груза на втором плече коромысло остаётся в равновесии при смещении его точки опоры от середины в сторону гирьки на у=1/3 его длины. Считая коромысло однородным по длине, найдите массу взвешиваемого груза m.

Решение. Для решения задачи воспользуемся правилом рычага. При взвешивании груза неизвестной массы 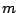на плечи коромысла длины 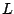действуют силы mg, Mg и mg, где m — масса коромысла (см. рис.). Плечи этих сил относительно оси, проходящей через точку опоры перпендикулярно плоскости рисунка, равны (0,5+x)L,

(0,5- x)L и 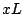соответственно. Условие равновесия рычага имеет вид:

mg(0,5+x)L + mgxL = Mg (0,5-x)L, откуда

m=[M (0,5-x)-mx]/(0,5+x)
Рассмотрим теперь второе взвешивание

(без груза неизвестной массы), которое позволит

нам найти массу коромысла. Плечи сил Mg и mg

будут теперь равны (0,5-y)L и yL соответственно.

Тогда условие равновесия рычага даёт:

mgyL = Mg(0,5-y)L, откуда m = M(0,5-y)/y

Следовательно, m = [M(0,5-y)- M(0,5-y)x/y]/(0,5+x)=

M(y-x)/y(1+2x)=M(1/3-1/4)3/(1+2/4)=M/6

Неоднородный рычаг

6.Петя решил определить массу учебника физики с помощью рычага. В распоряжении Пети имеется неоднородный по плотности рычаг, груз массой m₁ =100 г с крючком, и, учебник по физике массой m₂.

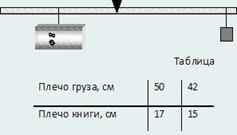
Петя собрал экспериментальную установку (смотри рисунок), и стал проводить измерения (смотри таблицу). Определите массу учебника, пользуясь данными полученными Петей.
Можно ли по данным таблицы определить массу рычага?
Примечание: если неоднородный по плотности рычаг подвесить за середину, то он не будет в равновесии.

Решение. Так как рычаг неоднородный, то он не будет в равновесии, если его подвесить за середину. Запишем условие равновесия рычага в первом случае:
m₁gl₁ + mgx = m₂gl₂. (1)

Так, как заведомо известно, что учебник имеет большую массу чем груз в 100 г, то равновесие возможно, когда центр масс (тяжести) находится правее точки подвеса.
Во втором случае m₁gl₁^/ + mgx = m₂gl₂^/. (2)

Из (1) уравнения вычтем (2): m₁(l₁ − l₁^/) = m₂(l₂ − 1₂^/),

тогда искомая масса учебника m₂ = (l₁ − l₁^/)/(l₂ − 1₂^/) × m₁. (3)

После вычисления: m₂ = (50 − 42)/(17 − 15) × 100 г = 400 г.

Определить массу рычага по данным таблицы нельзя. Так как в уравнении (1) или (2) две неизвестные: масса рычага и его плечо.

⇐ Предыдущая 123 4 5 Следующая ⇒